Question

【题目】已知，点分别为两条平行线上的一点，于.

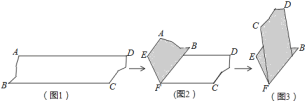
（1）如图1，直接写出和之间的数量关系；

（2）如图2，连接，过点分别作和的角平分线交于点，.

①求的度数；

②探究和的数量关系并加以证明.

Answer 1

【答案】（1），（2）①45°；②，证明见解析.

【解析】

（1）结论：∠ECD=90°+∠ABE．如图1中，过拐点作平行线，利用平行线性质即可得出结论；

（2） ①由和为和的角平分线，可得，再由，通过角的运算即可得出结论.

②由AB∥CD可得，再由，通过角的代换即可得出结论.

解：（1）结论：，

理由：如图1中，从过G点作GH平行CD，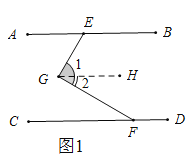

∵AB∥CD，

∴AB∥CD∥GH
∴∠AEG=∠1，∠CFG=∠2，
∵GE⊥GF，
∴∠CEH=90°，
∴∠ECD=∠H+∠CEH=90°+∠H，
∴∠ECD=90°+∠ABE．

（2）

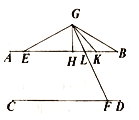
①∵

∴，

∵和为和的角平分线，

∴，

∵，

∴，

∴；

②结论：.

∵，

∴，

∴，

∵，

∴，

∴，

∵，

∴，

∴.