题目内容
如图,四边形OABC是面积为4的正方形,函数![]() (x>0)的图象经过点B.
(x>0)的图象经过点B.

(1)求k的值;
(2)将正方形OABC分别沿直线AB、BC翻折,得到正方形MABC′、MA′BC.设线段MC′、NA′分别与函数![]() (x>0)的图象交于点E、F,求线段EF所在直线的解析式.
(x>0)的图象交于点E、F,求线段EF所在直线的解析式.
(1)4(2) ![]()
解析:(1)∵四边形OABC是面积为4的正方形,
∴OA=OC=2,
∴点B坐标为(2,2),
∴k=xy=2×2=4………3分
(2))∵正方形MABC′、NA′BC由正方形OABC翻折所得,
∴ON=OM=2OA=4,
∴点E横坐标为4,点F纵坐标为4.
∵点E、F在函数y=4x 的图象上,
∴当x=4时,y=1,即E(4,1),
当y=4时,x=1,即F(1,4).
∴![]() ………8分
………8分
(1)根据正方形的面积公式可求得点B的坐标,从而求得k值
(2)先根据正方形的性质求得点F的纵坐标和点E的横坐标,代入反比例函数解析式求得其坐标,进而得出线段EF所在直线的解析式

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
 动.过点N作NP⊥OA于点P,连接AC交NP于Q,连接MQ.
动.过点N作NP⊥OA于点P,连接AC交NP于Q,连接MQ.  在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点.
在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点.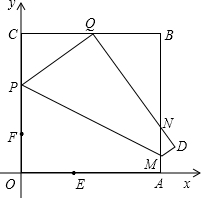
 (2012•呼伦贝尔)如图,四边形OABC是边长为2的正方形,反比例函数
(2012•呼伦贝尔)如图,四边形OABC是边长为2的正方形,反比例函数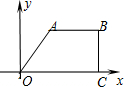 是( )
是( )