题目内容
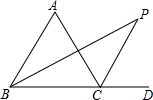 如图,△ABC的内角平分线BP与外角平分线CP交于P,试探究∠A与∠P之间的数量关系.
如图,△ABC的内角平分线BP与外角平分线CP交于P,试探究∠A与∠P之间的数量关系.
解:∵△ABC的内角平分线BP与外角平分线CP交于P,
∴∠PBC= ∠ABC,∠PCD=
∠ABC,∠PCD= ∠ACD,
∠ACD,
∵∠ACD=∠A+∠ABC,∠PCD=∠PBC+∠P,
∴ (∠A+∠ABC)=∠PBC+∠P=
(∠A+∠ABC)=∠PBC+∠P= ∠ABC+∠P,
∠ABC+∠P,
∴∠P= ∠A.
∠A.
分析:根据角平分线的定义得∠PBC= ∠ABC,∠PCD=
∠ABC,∠PCD= ∠ACD,再根据三角形外角性质得∠ACD=∠A+∠ABC,∠PCD=∠PBC+∠P,所以
∠ACD,再根据三角形外角性质得∠ACD=∠A+∠ABC,∠PCD=∠PBC+∠P,所以 (∠A+∠ABC)=∠PBC+∠P=
(∠A+∠ABC)=∠PBC+∠P= ∠ABC+∠P,然后整理可得∠P=
∠ABC+∠P,然后整理可得∠P= ∠A.
∠A.
点评:本题考查了三角形内角和定理:三角形内角和是180°.也考查了三角形外角性质.
∴∠PBC=
 ∠ABC,∠PCD=
∠ABC,∠PCD= ∠ACD,
∠ACD,∵∠ACD=∠A+∠ABC,∠PCD=∠PBC+∠P,
∴
 (∠A+∠ABC)=∠PBC+∠P=
(∠A+∠ABC)=∠PBC+∠P= ∠ABC+∠P,
∠ABC+∠P,∴∠P=
 ∠A.
∠A.分析:根据角平分线的定义得∠PBC=
 ∠ABC,∠PCD=
∠ABC,∠PCD= ∠ACD,再根据三角形外角性质得∠ACD=∠A+∠ABC,∠PCD=∠PBC+∠P,所以
∠ACD,再根据三角形外角性质得∠ACD=∠A+∠ABC,∠PCD=∠PBC+∠P,所以 (∠A+∠ABC)=∠PBC+∠P=
(∠A+∠ABC)=∠PBC+∠P= ∠ABC+∠P,然后整理可得∠P=
∠ABC+∠P,然后整理可得∠P= ∠A.
∠A.点评:本题考查了三角形内角和定理:三角形内角和是180°.也考查了三角形外角性质.

练习册系列答案
相关题目
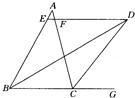 105、如图,△ABC的内角∠ABC的平分线与外角∠ACG的平分线交于点D,过点D作BC的平行线交AB于E,交AC于F.试判断EF与BE,CF之间的关系,并说明理由.
105、如图,△ABC的内角∠ABC的平分线与外角∠ACG的平分线交于点D,过点D作BC的平行线交AB于E,交AC于F.试判断EF与BE,CF之间的关系,并说明理由. 如图,△ABC的内角平分线BP与外角平分线CP交于P,试探究∠A与∠P之间的数量关系.
如图,△ABC的内角平分线BP与外角平分线CP交于P,试探究∠A与∠P之间的数量关系. 如图,△ABC的两内角平分线相交于点D,∠A=50°,则∠D=
如图,△ABC的两内角平分线相交于点D,∠A=50°,则∠D=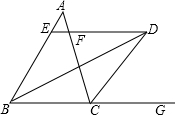 如图,△ABC的内角∠ABC的平分线与外角∠ACG的平分线交于点D,过点D作BC的平行线交AB于E,交AC于F.试判断EF与BE,CF之间的关系,并说明理由.
如图,△ABC的内角∠ABC的平分线与外角∠ACG的平分线交于点D,过点D作BC的平行线交AB于E,交AC于F.试判断EF与BE,CF之间的关系,并说明理由.