题目内容
如图，四边形OABC中，OA=OB=OC，∠2是∠1的4倍，那么∠4是∠3的________倍．
4
分析：四边形OABC中，由于OA=OB=OC，那么A、B、C必在以O为圆心，OA为半径的圆上；构建出此圆，然后利用圆心角与圆周角之间的关系求解．
解答：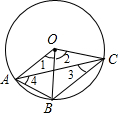
解：∵四边形OABC中，OA=OB=OC，
∴A、B、C在以O为圆心，以OA为半径的圆上；（如图）
∵∠2=4∠1，∠4=
∠2，∠3=∠1，
∴∠4=4∠3；
故∠4是∠3的4倍．
点评：解答此题的关键是先确定A、B、C三点共圆，再根据圆周角定理确定∠3，∠4的倍数关系．
分析：四边形OABC中，由于OA=OB=OC，那么A、B、C必在以O为圆心，OA为半径的圆上；构建出此圆，然后利用圆心角与圆周角之间的关系求解．
解答：
解：∵四边形OABC中，OA=OB=OC，∴A、B、C在以O为圆心，以OA为半径的圆上；（如图）
∵∠2=4∠1，∠4=
∠2，∠3=∠1，∴∠4=4∠3；
故∠4是∠3的4倍．
点评：解答此题的关键是先确定A、B、C三点共圆，再根据圆周角定理确定∠3，∠4的倍数关系．
练习册系列答案
相关题目
动．过点N作NP⊥OA于点P，连接AC交NP于Q，连接MQ． 
在MN上，并与MN上的点G重合，折痕为EF，点F为折痕与y轴的交点．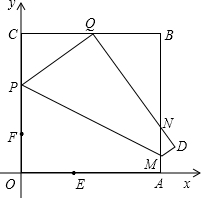
（2012•呼伦贝尔）如图，四边形OABC是边长为2的正方形，反比例函数
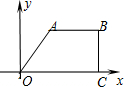是（ ）