题目内容
手工制作小组有若干人,他们将自己制作的手工艺品向本组成员各赠送一件,已知全组共互赠手工艺品90件,求该小组有多少位同学?
考点:一元二次方程的应用
专题:
分析:先求每名同学赠的手工艺品,再求x名同学赠的手工艺品,而已知全组共互赠了72件,故根据等量关系可得到方程.
解答:解:设生物兴趣小组有x名同学,
则每名同学所赠的手工艺品为:(x-1)件,
那么x名同学共赠:x(x-1)件,
所以,x(x-1)=90.
解得:x1=-9(不合题意舍去),x2=10,
答:生物兴趣小组有10名同学.
则每名同学所赠的手工艺品为:(x-1)件,
那么x名同学共赠:x(x-1)件,
所以,x(x-1)=90.
解得:x1=-9(不合题意舍去),x2=10,
答:生物兴趣小组有10名同学.
点评:本题考查了一元二次方程的实际运用:要全面、系统地弄清问题的已知和未知,以及它们之间的数量关系,找出并全面表示问题的相等关系,设出未知数,用方程表示出已知量与未知量之间的等量关系,即列出一元二次方程.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 如图,△ABC≌△BAD,如果AB=6cm,BD=4cm,AD=5cm,那么BC的长是( )
如图,△ABC≌△BAD,如果AB=6cm,BD=4cm,AD=5cm,那么BC的长是( )| A、4cm | B、5cm |
| C、6cm | D、无法确定 |
在方程x2+x=y,
x-2x2=3,(x-1)(x-2)=0,x2-
=4,x(x-1)=1中,一元二次方程的个数是( )
| 5 |
| 1 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
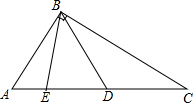 如图,在Rt△ABC中,∠ABC=90°,D、E在AC上,且AB=AD,CB=CE.
如图,在Rt△ABC中,∠ABC=90°,D、E在AC上,且AB=AD,CB=CE. 已知在矩形ABCD中,AC,BD交于点O,AE⊥BD于E,若OE:ED=1:3,AE=
已知在矩形ABCD中,AC,BD交于点O,AE⊥BD于E,若OE:ED=1:3,AE=