Question

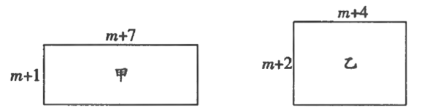
【题目】甲、乙两个长方形的边长如图所示(为正整数)，其面积分别为.

(1)填空: (用含的代数式表示)；

(2)若一个正方形的周长等于甲、乙两个长方形的周长之和.

①设该正方形的边长为，求的值(用含的代数式表示)；

②设该正方形的面积为，试探究: 与的差是否是常数?若是常数，求出这个常数，若不是常数，请说明理由，

(3)若另一个正方形的边长为正整数，并且满足条件的有且只有4个，求的值.

Answer 1

【答案】（1）2m-1；（2）①x的值为：2m+7；②与的差是常数，这个常数是19；（3）m的值为3.

【解析】

（1）根据长方形的面积公式分别求出，再作差即可得出答案；

（2）①根据长方形的周长公式求出甲乙两个长方形的周长，再根据正方形的周长公式求出x，即可得出答案；②利用①求出的x，求出正方形的面积，代入化简即可得出答案；

（3） 根据题意求出的取值范围，即得到2m-1的取值范围，根据取值范围求出m的值，再根据m是正整数这一条件得出m的值.

解：（1）由题意可得：

∴

（2）①∵正方形的周长等于甲、乙两个长方形的周长之和

∴正方形的周长=2(m+7+m+1)+2(m+4+m+2)=8m+28

又正方形的边长为

∴4x=8m+28

解得：x=2m+7

∴x的值为：2m+7.

②由①可知，

∴

故与的差是常数，这个常数是19.

（3）∵的有且只有4个

∴

即4<2m-1≤5

解得：

又m为正整数

∴m=3

故m的值为3.