题目内容
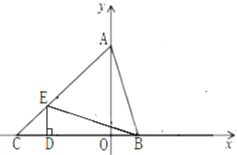
【题目】在平面直角坐标系中，已知A（1，1）、B（3，5），要在坐标轴上找一点
，使得△PAB的周长最小，则点的坐标为（ ）
A.
B.
C.
或D.或
【答案】B
【解析】
由题意可知：△PAB的周长最小就是PA＋PB最小，根据P点在坐标轴上分类讨论：①若P在y轴上，作A关于y轴的对称点
，连接
，交y轴于点P，根据两点之间，线段最短即可得此时P点即为所求，然后利用待定系数法求出直线的解析式，从而求出P点坐标，同时求出此时的长度；②若P在x轴上，原理同上，求出此时P点坐标，并同时求出此时的长度，然后比较①②中两个的长度的大小，即可判断哪种情况△PAB的周长最小，从而判断出P点坐标.
解：∵AB的长度固定
∴△PAB的周长最小就是PA＋PB最小
①若P在y轴上，如下图所示，作A关于y轴的对称点，连接，交y轴于点P
根据对称的性质：PA＋PB=
，根据两点之间，线段最短，可知此时PA＋PB最小，且最小值即为的长度，
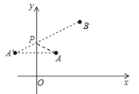
∵A点坐标为（1，1）
∴点的坐标为（﹣1,1）
设直线的解析式为y=kx＋b，将
的坐标代入得：
解得：
∴直线的解析式为y=x＋2
当x=0时，y=2
∴此时P点坐标为（0,2）
②若P在x轴上，如下图所示，作A关于x轴的对称点，连接，交x轴于点P
根据对称的性质：PA＋PB=，根据两点之间，线段最短，可知此时PA＋PB最小，且最小值即为的长度，
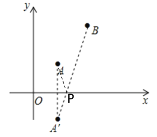
∵A点坐标为（1，1）
∴点的坐标为（1,﹣1）
设直线的解析式为y=kx＋b，将的坐标代入得：
解得：
∴直线的解析式为y=3x－4
当y=0时，x=
∴此时P点坐标为（,0）
∵
∴当P在y轴上时，的长最小
∴P点坐标为（0,2）
故选B.
练习册系列答案
相关题目
