题目内容
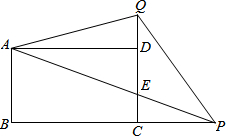 如图,P、Q是矩形ABCD的边BC和CD延长线上的两点,AP与CQ相交于点E,且∠PAD=∠QAD,求证:
如图,P、Q是矩形ABCD的边BC和CD延长线上的两点,AP与CQ相交于点E,且∠PAD=∠QAD,求证:(1)∠BAP=∠AQE;
(2)S△APQ=S矩形ABCD.
分析:(1)根据等角的余角相等证明即可;
(2)利用“角边角”证明△ADQ和△ADE全等,根据全等三角形对应边相等可得DQ=DE,再根据两组角对应相等,两三角形相似求出△ABP和△QDA相似,根据相似三角形对应边成比例列式表示出DQ,然后根据S△APQ=S△AQE+S△PQE列式整理即可得证.
(2)利用“角边角”证明△ADQ和△ADE全等,根据全等三角形对应边相等可得DQ=DE,再根据两组角对应相等,两三角形相似求出△ABP和△QDA相似,根据相似三角形对应边成比例列式表示出DQ,然后根据S△APQ=S△AQE+S△PQE列式整理即可得证.
解答:证明:(1)∵∠PAD+∠BAP=90°,∠QAD+∠AQE=90°,
∠PAD=∠QAD,
∴∠BAP=∠AQE;
(2)在△ADQ和△ADE中,
,
∴△ADQ≌△ADE(ASA),
∴DQ=DE,
∵∠BAP=∠AQE,∠B=∠ADQ=90°,
∴△ABP∽△QDA,
∴
=
,
∴DQ=
,
∵S△APQ=S△AQE+S△PQE,
=
QE•BC+
QE•CP,
=
QE•PB,
=
×(2DQ)•PB,
×
•PB,
=AB•AD,
∴S△APQ=S矩形ABCD.
∠PAD=∠QAD,
∴∠BAP=∠AQE;
(2)在△ADQ和△ADE中,
|
∴△ADQ≌△ADE(ASA),
∴DQ=DE,
∵∠BAP=∠AQE,∠B=∠ADQ=90°,
∴△ABP∽△QDA,
∴
| AB |
| DQ |
| PB |
| AD |
∴DQ=
| AB•AD |
| PB |
∵S△APQ=S△AQE+S△PQE,
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 2AB•AD |
| PB |
=AB•AD,
∴S△APQ=S矩形ABCD.
点评:本题考查了矩形的性质,等角的余角相等的性质,全等三角形的判定与性质,相似三角形的判定与性质,(2)把△APQ的面积分成两个三角形的面积的和求解是解题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 24、如图,已知P是矩形ABCD的内的一点.求证:PA2+PC2=PB2+PD2.
24、如图,已知P是矩形ABCD的内的一点.求证:PA2+PC2=PB2+PD2.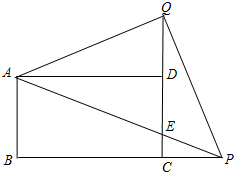 如图,P、Q是矩形ABCD的边BC和CD延长上的两点,AP与CQ相交于点E,且∠PAD=∠QAD,则①DQ=DE;②∠BAP=∠AQE;③AQ⊥PQ;④EQ=2CP;⑤S△APQ=S矩形ABCD.下列四个结论中正确的是( )
如图,P、Q是矩形ABCD的边BC和CD延长上的两点,AP与CQ相交于点E,且∠PAD=∠QAD,则①DQ=DE;②∠BAP=∠AQE;③AQ⊥PQ;④EQ=2CP;⑤S△APQ=S矩形ABCD.下列四个结论中正确的是( ) (2011•本溪一模)如图,四边形ABCD中是矩形,把这个矩形沿直线AC折叠,点B落在点E处,若∠DAC=50°,则∠EAC等于
(2011•本溪一模)如图,四边形ABCD中是矩形,把这个矩形沿直线AC折叠,点B落在点E处,若∠DAC=50°,则∠EAC等于 如图所示,OACB是矩形,C(a,b),点D为BC中点,反比例函数y=
如图所示,OACB是矩形,C(a,b),点D为BC中点,反比例函数y=