题目内容
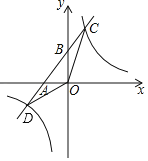
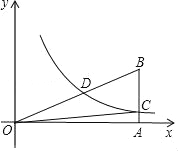
【题目】如图，在平面直角坐标系
中，已知直线
与x轴交于点A，与y轴交于点B，过A、B两点的抛物线
与x轴交于另一点
．
（1）求抛物线的解析式；
（2）在抛物线上是否存在一点P，使
？若存在，请求出点P的坐标，若不存在，请说明理由；
（3）点M为直线
下方抛物线上一点，点N为y轴上一点，当
的面积最大时，求
的最小值．
【答案】（1）
；（2）存在点P，坐标为（2，-3）；（3）
【解析】
（1）分别求出A、B坐标，然后将A、B、C三点坐标代入抛物线，即可得出其解析式；
（2）首先假设存在点P，然后根据面积相等构建等式，看是否有解，即可得解；
（3）首先设点M坐标，根据面积最大构建二次函数求最大值得出点M坐标，然后设点N坐标，再次构建二次函数求最小值，即可得解．
（1）由题意，令
，即
∴A的坐标为（4,0）
令
，即
∴B的坐标为（0，-2）
将A、B、C三点坐标代入抛物线，得
解得
∴抛物线解析式为：；
（2）假设存在该点P，设其坐标为（a，
）
∵A的坐标为（4,0），B的坐标为（0，-2）
∴OA=4，OB=2，
，
∴点P到直线
的距离为
∵
∴
∴
∴存在这样的点P，点P的坐标为（2，-3）
（3）设M坐标为
当
的面积最大时，即
的面积最大为4，
∴M坐标为
设N的坐标为
当
时，
有最小值，
其值为.
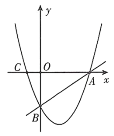
小学生10分钟口算测试100分系列答案
【题目】在初中阶段的函数学习中，我们经历了列表、描点、连线画函数图象，并结合图象研究函数性质的过程．以下是我们研究函数
性质及其应用的部分过程，请按要求完成下列各小题．
（1）请把下表补充完整，并在图中补全该函数图象；
| … | －5 | －4 | －3 | －2 | －1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
| … |
|
|
| －3 | 0 | 3 |
|
|
| … |
（2）根据函数图象，判断下列关于该函数性质的说法是否正确，正确的在相应的括号内打“√”，错误的在相应的括号内打“×”；
①该函数图象是轴对称图形，它的对称轴为y轴；( )
②该函数在自变量的取值范围内，有最大值和最小值，当
时，函数取得最大值3；当
时，函数取得最小值－3；( )
③当
或
时，y随x的增大而减小；当
时，y随x的增大而增大；( )
（3）已知函数
的图象如图所示，结合你所画的函数图象，直接写出不等式
的解集（保留1位小数，误差不超过0.2）．
【题目】争创全国文明城市，从我做起．尚理中学在八年级开设了文明礼仪校本课程，为了解学生的学习情况，随机抽取了20名学生的测试成绩，分数如下：
94 83 90 86 94 88 96 100 89 82
94 82 84 89 88 93 98 94 93 92
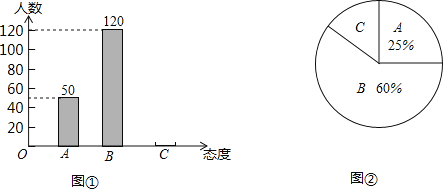
整理上面的数据，得到频数分布表和扇形统计图：
等级 | 成绩/分 | 频数 |
A |
| a |
B |
| 8 |
C |
| 5 |
D |
| 4 |
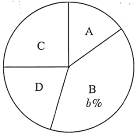
根据以上信息，解答下列问题．
（1）填空：
_______，
______；
（2）若成绩不低于90分为优秀，估计该校1200名八年级学生中，达到优秀等级的人数；
（3）已知A等级中有2名女生，现从A等级中随机抽取2名同学，试用列表或画树状图的方法求出恰好抽到一男一女的概率．
