Question

【题目】在一堂数学实践课上，赵老师给出了下列问题：

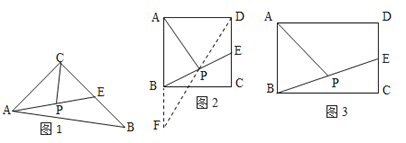
提出问题

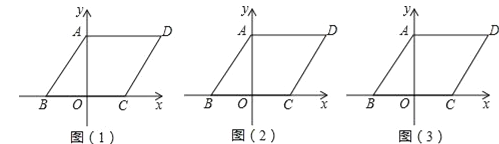
（1）如图1，在△ABC中，E是BC的中点，P是AE的中点，就称CP是△ABC的“双中线”，∠ACB＝900，AC＝3，AB＝5．则CP＝___；

探究规律

（2）在图2中，E是正方形ABCD一边上的中点，P是BE上的中点，则称AP是正方形ABCD的“双中线”，若AB＝4．则AP的长为_____；

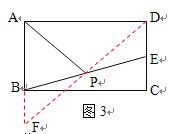
（3）在图3中，AP是矩形ABCD的“双中线”， 若AB＝4，BC＝6，请仿照（2）中的方法求出AP的长，并说明理由；

Answer 1

【答案】（1）；（2）；（3）AP＝3

【解析】

（1）先根据勾股定理求出BC=4，再根据双中线的定义得到E是BC的中点，故EC=2，利用勾股定理求出AE=，再根据直角三角形斜边上的中线求出CP的长；

（2）根据图中辅助线可证明△DEP≌△FBP，得到DE=BF,利用勾股定理求出DF的长，即可求出AP的长；

（3）连接DP并延长交AB的延长线于F ，证明△BPF≌△EPD，在Rt△ADF中，求出DF，在Rt△ADF中，求出AP.

解：（1）在Rt△ABC中，BC=,

∵CP是△ABC的“双中线”，

∴E是BC的中点，故EC=2，

在Rt△ACE中，AE=

又P是AE中点，

所以CP＝AE= ；

（2）如图2，连接DP，交AB延长线与F，∵CD∥AB,∴∠F=∠PDE, ∠PBF=∠PED,

又P是BE中点，∴BP=EP，∴△DEP≌△FBP

∴DE=BF

故AF=4+2=6，

在Rt△ADF中，DF=

又P为DF中点，∴AP=DF=

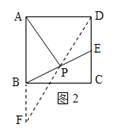
∴AP的长为；

（3）连接DP并延长交AB的延长线于F

∵矩形ABCD

∴AB∥CD

∴∠PBF＝∠PED，∠F＝∠PDE

∵P是BE的中点

∴PB＝PE

∴△BPF≌△EPD

∴BF＝DE＝CD＝2

在Rt△ADF中

DF＝

＝

＝6

在Rt△ADF中

AP＝DF＝3