Question

【题目】在△ABC中，AC=6 ，点D为直线AB上一点，且AB=3BD，直线CD与直线BC所夹锐角的正切值为 ，并且CD⊥AC，则BC的长为________．

Answer 1

【答案】 或15

【解析】

如图1中，当点D在AB的延长线上时，作BE⊥CD垂足为E，先求出BE，EC，在RT△BCE中利用勾股定理即可解决，如图2中，当点D在线段AB上时，作BE⊥CD于E，方法类似第一种情形．

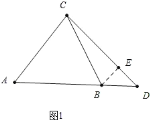
解：如图1中，当点D在AB的延长线上时，作BE⊥CD垂足为E，

∵AC⊥CD，

∴AC∥BE，

∴，

∵AC＝，

∴BE＝，

∵tan∠BCE＝，

∴EC＝2BE＝，

∴BC＝ ．

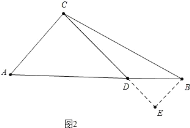
如图2中，当点D在线段AB上时，作BE⊥CD于E，

∵AC∥BE，AC＝，

∴，

∴BE=，

∵tan∠BCE＝，

∴EC＝2BE＝，

∴BC＝

故答案为：或15．