Question

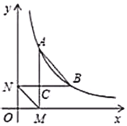
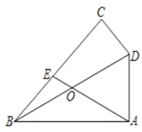
【题目】如图，在四边形ABCD中，∠BAD＝∠BCD＝90°，∠ABC＝45°，连接BD，点O为BD的中点，连接AO并延长交BC于点E，若，CD＝4，则AD的长为_____．

Answer 1

【答案】

【解析】

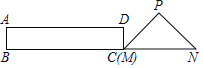
延长BC，AD交于F，过D作DS∥BC交AE于S，过A作AH⊥BF于H，设BE＝3m，CE＝5m，得到BC＝8m，根据全等三角形的性质得到DS＝BE＝3m，求得CF＝CD＝4，得到DF＝4，BF＝8m+4，根据相似三角形的性质即可得到结论．

解：延长BC，AD交于F，过D作DS∥BC交AE于S，过A作AH⊥BF于H，

∵，

∴设BE＝3m，CE＝5m，

∴BC＝8m，

∵点O为BD的中点，

∴BO＝DO，

∵DS∥BE，

∴∠EBO＝∠SDO，

∵∠BOE＝∠DOS，

∴△BOE≌△DOS（ASA），

∴DS＝BE＝3m，

∵∠BAD＝∠BCD＝90°，∠ABC＝45°，

∴∠F＝45°，

∴△ABF和△DCF是等腰直角三角形，

∴CF＝CD＝4，

∴DF＝4，BF＝8m+4，

∴BH＝FH＝BF＝4m+2，AF＝BF＝4m+2；

∴EF＝BF﹣BE＝5m+4，AD＝4m﹣2，

∵DS∥EF，

∴△ADS∽△AFE，

∴，

∴，

解得：m＝1（经检验后，负值舍去），

∴AD的长为2，

故答案为：2．