题目内容
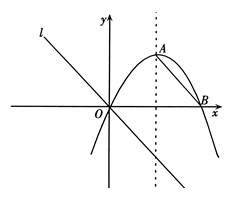
如图,对称轴为 的抛物线
的抛物线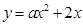 与
与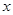 轴相交于点
轴相交于点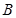 、
、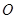 .
.
【小题1】求抛物线的解析式,并求出顶点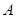 的坐标;
的坐标;
【小题2】连结AB,把AB所在的直线平移,使它经过原点O,得到直线l.点P是l上一动点.设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为 ,当0<S≤18时,求
,当0<S≤18时,求 的取值范围;
的取值范围;
【小题3】在(2)的条件下,当 取最大值时,抛物线上是否存在点
取最大值时,抛物线上是否存在点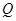 ,使△OP
,使△OP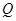 为直角三角形且OP为直角边.若存在,直接写出点
为直角三角形且OP为直角边.若存在,直接写出点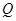 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【小题1】(1)∵点B与O(0,0)关于x=3对称,
∴点B坐标为(6,0).
将点B坐标代入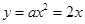 得:
得:
36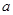 +12=0,
+12=0,
∴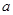 =
=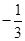 .
.
∴抛物线解析式为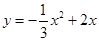 .
.
当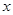 =3时,
=3时, ,
,
∴顶点A坐标为(3,3).
(说明:可用对称轴为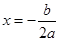 ,求
,求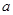 值,用顶点式求顶点A坐标.)
值,用顶点式求顶点A坐标.)
【小题2】(2)设直线AB解析式为y=kx+b.
∵A(3,3),B(6,0),
∴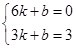 解得
解得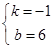 , ∴
, ∴ .
.
∵直线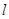 ∥A
∥A B且过点O,
B且过点O,
∴直线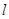 解析式为
解析式为 .
.
∵点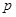 是
是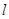 上一动点且横坐标为
上一动点且横坐标为 ,
,
∴点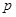 坐标为(
坐标为(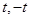 )
)
当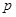 在第四象限时(t>0),
在第四象限时(t>0),
=12×6×3+ ×6×
×6×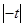
=9+3 .
.
∵0<S≤18,
∴0<9+3 ≤18,
≤18,
∴-3< ≤3.
≤3.
又 >0,
>0,
∴0<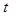 ≤3.5分
≤3.5分
当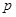 在第二象限时(
在第二象限时( <0),
<0),
作PM⊥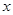 轴于M,设对称轴与
轴于M,设对称轴与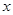 轴交点为N.
轴交点为N. 
则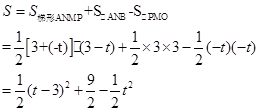
=-3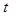 +9.
+9.
∵0<S≤18,
∴0<-3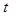 +9≤18,
+9≤18,
∴-3≤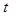 <3.
<3.
又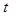 <0,
<0,
∴-3≤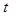 <0.6分
<0.6分
∴t的取值范围是-3≤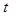 <0或0<
<0或0<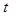 ≤3.
≤3.
【小题3】(3)存在,点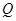 坐标为(3,3)或(6,0)或(-3,-9)
坐标为(3,3)或(6,0)或(-3,-9)
解析

练习册系列答案
相关题目
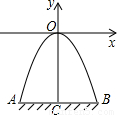
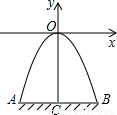
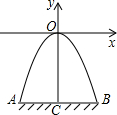 如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系,
如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系,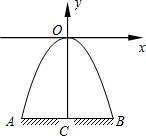 如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系.求:
如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系.求: (2)有一辆宽2.8米,高1米的农用货车(货物最高处与地面AB的距离)能否通过此隧道?
(2)有一辆宽2.8米,高1米的农用货车(货物最高处与地面AB的距离)能否通过此隧道?