题目内容
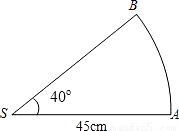
 如图,扇形彩色纸的半径为45cm,圆心角为40°,用它制作一个圆锥形火炬模型的侧面(接头忽略不计),则这个圆锥的高约为
如图,扇形彩色纸的半径为45cm,圆心角为40°,用它制作一个圆锥形火炬模型的侧面(接头忽略不计),则这个圆锥的高约为(结果精确到0.1cm.参考数据:
| 2 |
| 3 |
| 5 |
分析:先根据圆锥的底面周长等于侧面展开图的扇形弧长是10π,求出半径,再根据勾股定理计算.
解答:解:扇形的弧长是:
=10π,
设圆锥的底面半径是r,
则2πr=10π,
解得:r=5cm,
圆锥的母线,锥高,底面半径正好构成直角三角形,
根据勾股定理就可以得到圆锥的高=
=
=20
≈44.7cm.
这个圆锥的高约为44.7cm.
| 40π•45 |
| 180 |
设圆锥的底面半径是r,
则2πr=10π,
解得:r=5cm,
圆锥的母线,锥高,底面半径正好构成直角三角形,
根据勾股定理就可以得到圆锥的高=
| 452-52 |
| 2000 |
| 5 |
这个圆锥的高约为44.7cm.
点评:本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:
(1)圆锥的母线长等于侧面展开图的扇形半径;
(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.
(1)圆锥的母线长等于侧面展开图的扇形半径;
(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.

练习册系列答案
相关题目
 ,用它制作一个圆锥形火炬模型的侧面(接头忽略不计),则这个圆锥的高约为 cm.(结果精确到0.1cm.参考数据:
,用它制作一个圆锥形火炬模型的侧面(接头忽略不计),则这个圆锥的高约为 cm.(结果精确到0.1cm.参考数据: ,
, ,
, ,
, )
)
 ≈1.414,
≈1.414, ≈1.732,
≈1.732, ≈2.236,π≈3.142)
≈2.236,π≈3.142)
 ≈1.414,
≈1.414, ≈1.732,
≈1.732, ≈2.236,π≈3.142)
≈2.236,π≈3.142)
 ≈1.414,
≈1.414,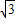 ≈1.732,
≈1.732,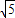 ≈2.236,π≈3.142)
≈2.236,π≈3.142)