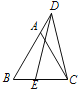题目内容
【题目】已知![]() ,
,![]() ,
,![]() 是
是![]() 边上一点,延长
边上一点,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 的垂直平分线于点
的垂直平分线于点![]() ,连接
,连接![]() .
.
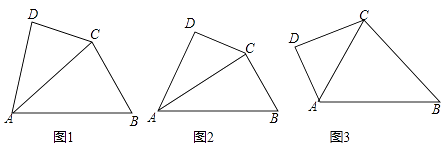
(1)如图1,当点![]() 与点
与点![]() 重合时,证明:
重合时,证明:![]() ;
;

(2)如图2,当点![]() 不与
不与![]() ,
,![]() 两点重合时,(1)中的结论是否还成立?并说明理由.
两点重合时,(1)中的结论是否还成立?并说明理由.
【答案】(1)见解析(2)成立,理由见解析
【解析】
(1)延长FD至点G,使得DG=DF,连接BG,AG.
先证明△ADG≌△EDF,得到AG=EF.再证明△ABG≌△DBF,得到∠ABG=∠DBF,即有∠ABG=∠DBG=![]() ∠ABC=30°,进而得到∠DBF=30°,根据30°角所对的直角边等于斜边的一半即可得到结论.
∠ABC=30°,进而得到∠DBF=30°,根据30°角所对的直角边等于斜边的一半即可得到结论.
(2)成立.延长FD至点![]() ,使得DG=DF,连接BG,AG.
,使得DG=DF,连接BG,AG.
通过证明△ADG≌△EDF,得到AG=EF.由垂直平分线的性质得到FC=FE,从而有AG=CF.
即可得到△ABG≌△CBF,由全等三角形对应角相等得到∠ABG=∠CBF,即有∠ABG=∠GBD.进而得出∠DBF=∠GBD=30°,根据30°角所对的直角边等于斜边的一半即可得到结论.
延长FD至点G,使得DG=DF,连接BG,AG.
∵DF⊥BC于点![]() ,∴∠BDF=90°,∴BG=BF,∴∠DBF=∠DBG.
,∴∠BDF=90°,∴BG=BF,∴∠DBF=∠DBG.
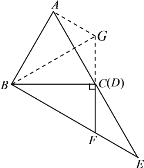
又∵AD=ED,∠ADG=∠EDF,DG=DF,∴△ADG≌△EDF(SAS),∴AG=EF.
∵点![]() 在CE的垂直平分线上,点
在CE的垂直平分线上,点![]() 与点
与点![]() 重合,∴DF=EF,∴DF=AG.
重合,∴DF=EF,∴DF=AG.
∵AB=BC,∴△ABG≌△DBF(SSS),∴∠ABG=∠DBF,∴∠ABG=∠DBG=![]() ∠ABC=30°,∴∠DBF=30°,∴BG=2DG,∴BF=2DF.
∠ABC=30°,∴∠DBF=30°,∴BG=2DG,∴BF=2DF.
(2)成立.理由如下:
延长FD至点![]() ,使得DG=DF,连接BG,AG.
,使得DG=DF,连接BG,AG.
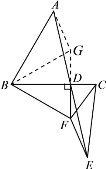
∵DF⊥BC于点![]() ,∴∠BDF=90°,∴BG=BF,∴∠DBF=∠DBG.
,∴∠BDF=90°,∴BG=BF,∴∠DBF=∠DBG.
又∵AD=ED,∠ADG=∠EDF,∴△ADG≌△EDF(SAS),∴AG=EF.
∵点![]() 在CE的垂直平分线上,∴FC=FE,∴AG=CF.
在CE的垂直平分线上,∴FC=FE,∴AG=CF.
又∵AB=BC,∴△ABG≌△CBF(SSS),∴∠ABG=∠CBF,∴∠ABG=∠GBD.
又∵∠ABC=60°,∴∠GBD=30°,∴∠DBF=∠GBD=30°,∴BF=2DF.