题目内容
15.变形与求值(1)通分:$\frac{x}{ac}$,$\frac{y}{bc}$.
(2)求值:$\frac{{{x^2}-2xy}}{{{x^2}-4xy+4{y^2}}}$,其中x=1,y=-$\frac{1}{2}$.
(3)不改变分式的值,变形使分式$\frac{{1-\frac{1}{2}x}}{x+1}$的分子与分母的最高次项的系数是正数.
分析 (1)根据通分的方法,先找出最简公分母即可解答本题;
(2)先化简题目中的式子,然后将x、y的值代入即可解答本题;
(3)先对题目中的式子变形即可解答本题.
解答 解:(1)通分:$\frac{x}{ac}=\frac{bx}{abc}$,$\frac{y}{bc}=\frac{ay}{abc}$;
(2)原式=$\frac{x(x-2y)}{{{{(x-2y)}^2}}}=\frac{x}{x-2y}$,
将x=1,$y=-\frac{1}{2}$代入得,
原式=$\frac{1}{1-2×(-\frac{1}{2})}=\frac{1}{2}$;
(3)原式=$\frac{2-x}{2x+2}$=$-\frac{x-2}{2x+2}$.
点评 本题考查分式的化简求值、通分,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
10.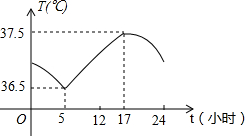 正常人的体温一般在37℃左右,但一天中的不同时刻不尽相同图反映了一天24小时内小明体温的变化情况,下列说法错误的是( )
正常人的体温一般在37℃左右,但一天中的不同时刻不尽相同图反映了一天24小时内小明体温的变化情况,下列说法错误的是( )
 正常人的体温一般在37℃左右,但一天中的不同时刻不尽相同图反映了一天24小时内小明体温的变化情况,下列说法错误的是( )
正常人的体温一般在37℃左右,但一天中的不同时刻不尽相同图反映了一天24小时内小明体温的变化情况,下列说法错误的是( )| A. | 清晨5时体温最低 | |
| B. | 下午5时体温最高 | |
| C. | 从5时至24时,小明体温一直是升高的 | |
| D. | 从0时至5时,小明体温一直是下降的 |
20.要使分式$\frac{1+m}{1-m}$有意义,则m的取值应满足( )
| A. | m≠1 | B. | m≠-1 | C. | m=1 | D. | m=-1 |
 如图,在△ABC中,∠B=38°,∠C=112°.
如图,在△ABC中,∠B=38°,∠C=112°.
 在数轴上描出表现下列各数的点,并用“<”把它们连接起来.
在数轴上描出表现下列各数的点,并用“<”把它们连接起来.