题目内容
已知x1=
+1是方程x2+mx+1=0的一个根,求m的值及方程的另一根.
| 2 |
考点:一元二次方程的解,根与系数的关系
专题:
分析:根据根的概念,将x1=
+1代入方程x2+mx+1=0,可求得m的值,再由根与系数的关系可求得方程的另一根.
| 2 |
解答:解:∵x1=
+1是方程x2+mx+1=0的一个根,
∴将x1=
+1代入方程x2+mx+1=0,得(
+1)2+(
+1)m+1=0,
解得m=-2
,
设方程的另一根根为x2,
∴x1+x2=-m=2
,
∴x2=
-1.
| 2 |
∴将x1=
| 2 |
| 2 |
| 2 |
解得m=-2
| 2 |
设方程的另一根根为x2,
∴x1+x2=-m=2
| 2 |
∴x2=
| 2 |
点评:本题考查了一元二次方程的解以及根与系数的关系,若x1,x2是一元二次方程ax2+bx+c=0的两根,则两根之和等于-
,两根之积等于
.
| b |
| a |
| c |
| a |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
计算(a3b)2的结果是( )
| A、a6b |
| B、a6b2 |
| C、a5b2 |
| D、a3b2 |

 如图,已知∠1=52°,∠2=128°,∠C=∠D,探索∠A与∠F的数量关系,并说明理由.
如图,已知∠1=52°,∠2=128°,∠C=∠D,探索∠A与∠F的数量关系,并说明理由.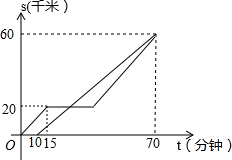 甲、乙两车都从A地前往B地,如图分别表示甲、乙两车离A地的距离S(千米)与时间t(分钟)的函数关系.已知甲车出发10分钟后乙车才出发,甲车中途因故停止行驶一段时间后按原速继续驶向B地,最终甲、乙两车同时到达B地,根据图中提供的信息解答下列问题:
甲、乙两车都从A地前往B地,如图分别表示甲、乙两车离A地的距离S(千米)与时间t(分钟)的函数关系.已知甲车出发10分钟后乙车才出发,甲车中途因故停止行驶一段时间后按原速继续驶向B地,最终甲、乙两车同时到达B地,根据图中提供的信息解答下列问题: