题目内容
 如图,直线l的解析式为y=
如图,直线l的解析式为y= x+4,l与x轴,y轴分别交于点A,B.
x+4,l与x轴,y轴分别交于点A,B.
(1)求原点O到直线l的距离;
(2)有一个半径为1的⊙C从坐标原点出发,以每秒1个单位长的速度沿y轴正方向运动,设运动时间为t(秒).当⊙C与直线l相切时,求t的值.
解:(1)在y= x+4中,令x=0,得y=4,得BO=4,令y=0,得x=-3,得AO=3,
x+4中,令x=0,得y=4,得BO=4,令y=0,得x=-3,得AO=3,
∴AB= =5
=5
设点O到直线AB的距离为h,
∵S△AOB= AO•BO=
AO•BO= AB•h
AB•h
∴h=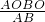 =2.4;
=2.4;
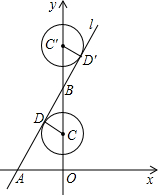
(2)如图,设⊙C与直线l相切于点D,连CD,则CD⊥AB,
∵AO⊥BO,∴∠BDC=∠BOA=90°
∵∠ABO=∠CBD
∴△ABO∽△CBD
∴ =
=
由(1)得AO=3,BO=4,AB=5
∴ =
=
∴BC=
∴OC=4- =
=
∴t=CO= (秒)
(秒)
根据对称性得BC'=BC=
∴OC'=4+ =
=
∴t=OC′= (秒)
(秒)
∴当⊙C与直线l相切时,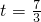 秒或
秒或 秒.
秒.
分析:(1)设点O到直线AB的距离为h,在y= x+4中,令x=0,得y=4,得BO=4,令y=0,得x=-3,得AO=3,有三角形的面积公式可求出O到直线AB的距离为h=2.4;
x+4中,令x=0,得y=4,得BO=4,令y=0,得x=-3,得AO=3,有三角形的面积公式可求出O到直线AB的距离为h=2.4;
(2)如图,设⊙C与直线l相切于点D,连CD,则CD⊥AB,由于AO⊥BO,∠ABO=∠CBD,所以∠BDC=∠BOA=90°,△ABO∽△CBD,故 =
= ,由(1)得AO=3,BO=4,AB=5,故
,由(1)得AO=3,BO=4,AB=5,故 =
= ,BC=
,BC= ,OC=4-
,OC=4- =
= ,t=CO=
,t=CO= (秒),根据对称性得BC'=BC=
(秒),根据对称性得BC'=BC= ,OC'=4+
,OC'=4+ =
= ,∴t=OC′=
,∴t=OC′= (秒).故当⊙C与直线l相切时,
(秒).故当⊙C与直线l相切时,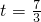 秒或
秒或 秒.
秒.
点评:此题把一次函数与圆的知识相结合,增加了难度,在解答此题时要注意直线与圆相切的两种情况,不要漏解.
 x+4中,令x=0,得y=4,得BO=4,令y=0,得x=-3,得AO=3,
x+4中,令x=0,得y=4,得BO=4,令y=0,得x=-3,得AO=3,∴AB=
 =5
=5设点O到直线AB的距离为h,
∵S△AOB=
 AO•BO=
AO•BO= AB•h
AB•h∴h=
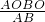 =2.4;
=2.4;
(2)如图,设⊙C与直线l相切于点D,连CD,则CD⊥AB,
∵AO⊥BO,∴∠BDC=∠BOA=90°
∵∠ABO=∠CBD
∴△ABO∽△CBD
∴
 =
=
由(1)得AO=3,BO=4,AB=5
∴
 =
=
∴BC=

∴OC=4-
 =
=
∴t=CO=
 (秒)
(秒)根据对称性得BC'=BC=

∴OC'=4+
 =
=
∴t=OC′=
 (秒)
(秒)∴当⊙C与直线l相切时,
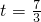 秒或
秒或 秒.
秒.分析:(1)设点O到直线AB的距离为h,在y=
 x+4中,令x=0,得y=4,得BO=4,令y=0,得x=-3,得AO=3,有三角形的面积公式可求出O到直线AB的距离为h=2.4;
x+4中,令x=0,得y=4,得BO=4,令y=0,得x=-3,得AO=3,有三角形的面积公式可求出O到直线AB的距离为h=2.4;(2)如图,设⊙C与直线l相切于点D,连CD,则CD⊥AB,由于AO⊥BO,∠ABO=∠CBD,所以∠BDC=∠BOA=90°,△ABO∽△CBD,故
 =
= ,由(1)得AO=3,BO=4,AB=5,故
,由(1)得AO=3,BO=4,AB=5,故 =
= ,BC=
,BC= ,OC=4-
,OC=4- =
= ,t=CO=
,t=CO= (秒),根据对称性得BC'=BC=
(秒),根据对称性得BC'=BC= ,OC'=4+
,OC'=4+ =
= ,∴t=OC′=
,∴t=OC′= (秒).故当⊙C与直线l相切时,
(秒).故当⊙C与直线l相切时,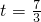 秒或
秒或 秒.
秒.点评:此题把一次函数与圆的知识相结合,增加了难度,在解答此题时要注意直线与圆相切的两种情况,不要漏解.

练习册系列答案
相关题目
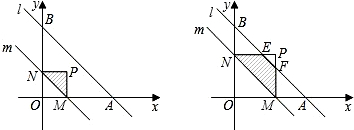

 如图,直线l的解析式为
如图,直线l的解析式为 如图,直线AB的解析式为y=
如图,直线AB的解析式为y= 求如图中直线L的解析式.
求如图中直线L的解析式.