题目内容
若等腰Rt△ABC内切圆半径为1，则该三角形的面积是________．
3+2
分析：设该等腰直角三角形的腰长为a，则斜边边长为a，根据切线的性质列出等式2（a-1）=a，求得a=2+，再根据面积公式计算即可．
解答：设该等腰直角三角形的腰长为a，则斜边边长为a，则
2（a-1）=a，
∴a=2+，
∴
=
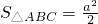=3+2．
故答案为：3+2．
点评：本题考查了三角形的内切圆和等腰直角三角形的性质，是基础知识要熟练掌握．
分析：设该等腰直角三角形的腰长为a，则斜边边长为
a，根据切线的性质列出等式2（a-1）=a，求得a=2+，再根据面积公式计算即可．解答：设该等腰直角三角形的腰长为a，则斜边边长为
a，则2（a-1）=
a，∴a=2+
，∴
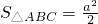==3+2．故答案为：3+2
．点评：本题考查了三角形的内切圆和等腰直角三角形的性质，是基础知识要熟练掌握．
练习册系列答案
相关题目
在第一象限内作等腰Rt△ABC，∠BAC=90°，点P（1，a）为坐标系内一动点．
（2012•拱墅区二模）已知二次函数y=-x2+4mx-8m+4：
限内作等腰Rt△ABC，∠BAC=90°，若点P（1，a）为坐标系中的一个动点．
如图所示，等腰Rt△ABC内一点D，若AD=2，BD=6，∠ADC=135°，则CD=________．