题目内容
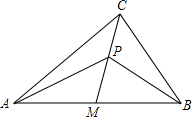 如图,在直角三角形ACB中,∠C=90°,已知AC=20cm,BC=15cm.
如图,在直角三角形ACB中,∠C=90°,已知AC=20cm,BC=15cm.
(1)求AB边的中线CM的长;
(2)在CM上取一点P(点P与点C、点M不重合),试求△APB的面积y(平方厘米)与CP的长x(厘米)之间的函数关系式;
(3)在直角坐标系中,画出函数的图象.
解:(1)∵∠C=90°,AC=20cm,BC=15cm,∴AB= =25,
=25,
在直角三角形中,根据斜边的中线长是斜边长的一半的性质,
∴CM= AB=
AB= (cm);
(cm);
(2)∵CP=x,CM=AM,∴∠CAB=∠ACM,
∵sin∠CAB= =
= ,∴sin∠ACM=
,∴sin∠ACM=
∴S△AMC= ×20×
×20× ×sin∠ACM=75,
×sin∠ACM=75,
S△ACP= ×20×x×
×20×x× =6x,∵△APB的面积y,
=6x,∵△APB的面积y,
∴ y=S△AMC-S△ACP=75-6x,
y=S△AMC-S△ACP=75-6x,
∴y=150-12x(0<x< );
);
(3)函数关系式为:y=150-12x(0<x< ),图象为:
),图象为:
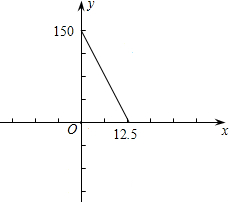
分析:(1)在直角三角形中,已知两直角边,根据勾股定理即可求斜边的长,根据斜边的中线长是斜边长的一半的性质即可以解题;
(2)根据S△AMP=S△ACM-S△APC即可求出 y,从而可得出答案;
y,从而可得出答案;
(3)根据函数关系式即可画出图象;
点评:本题考查了一次函数及勾股定理,难度较大,关键是掌握在直角三角形中,斜边的中线长是斜边长的一半.
 =25,
=25,在直角三角形中,根据斜边的中线长是斜边长的一半的性质,
∴CM=
 AB=
AB= (cm);
(cm);(2)∵CP=x,CM=AM,∴∠CAB=∠ACM,
∵sin∠CAB=
 =
= ,∴sin∠ACM=
,∴sin∠ACM=
∴S△AMC=
 ×20×
×20× ×sin∠ACM=75,
×sin∠ACM=75,S△ACP=
 ×20×x×
×20×x× =6x,∵△APB的面积y,
=6x,∵△APB的面积y,∴
 y=S△AMC-S△ACP=75-6x,
y=S△AMC-S△ACP=75-6x,∴y=150-12x(0<x<
 );
);(3)函数关系式为:y=150-12x(0<x<
 ),图象为:
),图象为: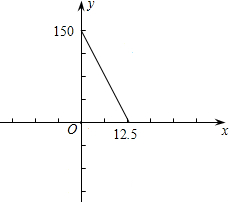
分析:(1)在直角三角形中,已知两直角边,根据勾股定理即可求斜边的长,根据斜边的中线长是斜边长的一半的性质即可以解题;
(2)根据S△AMP=S△ACM-S△APC即可求出
 y,从而可得出答案;
y,从而可得出答案;(3)根据函数关系式即可画出图象;
点评:本题考查了一次函数及勾股定理,难度较大,关键是掌握在直角三角形中,斜边的中线长是斜边长的一半.

练习册系列答案
相关题目
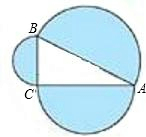 如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为( )
如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为( )| A、2π | B、3π | C、4π | D、6π |
 如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.
如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.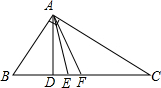 如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线,
如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线, 9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=
9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=