题目内容
如图,在梯形ABCD中,AD∥BC,E、F分别是AB、DC边的中点,AB=4,∠B=60°,(1)求点E到BC边的距离;
(2)点P为线段EF上的一个动点,过P作PM⊥BC,垂足为M,过点M作MN∥AB交线段AD于点N,连接PN、探究:当点P在线段EF上运动时,△PMN的面积是否发生变化?若不变,请求出△PMN的面积;若变化,请说明理由.
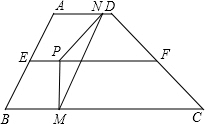
分析:(1)过E作EG⊥BC,垂足为G,由AB=4,E为AB的中点,得BE=2,又∠B=60°,解Rt△BEG可求EG,即为点E到BC边的距离;
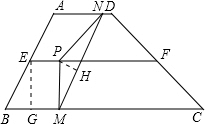
(2)过点P作PH⊥MN,垂足为H,根据平行关系,垂直关系推出∠PMH=30°,解Rt△PMH可求PH,再由面积公式求△PMN的面积.
(2)过点P作PH⊥MN,垂足为H,根据平行关系,垂直关系推出∠PMH=30°,解Rt△PMH可求PH,再由面积公式求△PMN的面积.
解答:解:(1)过E作EG⊥BC,垂足为G,由AB=4,E为AB的中点,得BE=2(1分)
Rt△EBG中,sin∠B=
,EG=EG•sin∠B=2sin∠60°=
;(2分)
(2)不变(1分)
解法(一):在梯形ABCD中,由AD∥BC,MN∥AB,得MN=AB=4(1分)
过点P作PH⊥MN,垂足为H(1分)
由MN∥AB得∠NMC=∠B=60°所以∠PMH=30°(1分)
由E、F是AB、DC边的中点得EF∥BC,由EG⊥BC,PM⊥BC,得EG∥PM
∴PM=EG=
(1分)
在Rt△PMH中,sin∠PMH=
,所以PH=PM•sin30°=
(2分)
∴S△PMN=
PH•MN=
×4×
=
.(2分)
解法(二):延长MP交AD于点H,只要求出NH的长即可,评分标准可参考解法一.
Rt△EBG中,sin∠B=
| EG |
| EB |
| 3 |

(2)不变(1分)
解法(一):在梯形ABCD中,由AD∥BC,MN∥AB,得MN=AB=4(1分)
过点P作PH⊥MN,垂足为H(1分)
由MN∥AB得∠NMC=∠B=60°所以∠PMH=30°(1分)
由E、F是AB、DC边的中点得EF∥BC,由EG⊥BC,PM⊥BC,得EG∥PM
∴PM=EG=
| 3 |
在Rt△PMH中,sin∠PMH=
| PH |
| PM |
| ||
| 2 |
∴S△PMN=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
解法(二):延长MP交AD于点H,只要求出NH的长即可,评分标准可参考解法一.
点评:本题考查了解梯形问题的转化方法,一般是将梯形问题转化为平行四边形、矩形、直角三角形来解题.

练习册系列答案
相关题目
 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )| A、3cm | B、7cm | C、3cm或7cm | D、2cm |
 11、如图,在梯形ABCD中,AB∥CD,对角线AC、BD交于点O,则S△AOD
11、如图,在梯形ABCD中,AB∥CD,对角线AC、BD交于点O,则S△AOD 已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10.
已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10. 如图,在梯形ABCD中,AD∥BC,AB⊥AD,对角线BD⊥DC.
如图,在梯形ABCD中,AD∥BC,AB⊥AD,对角线BD⊥DC. 20、如图,在梯形ABCD中,AD∥BC,并且AB=8,AD=3,CD=6,并且∠B+∠C=90°,则梯形面积S梯形ABCD=
20、如图,在梯形ABCD中,AD∥BC,并且AB=8,AD=3,CD=6,并且∠B+∠C=90°,则梯形面积S梯形ABCD=