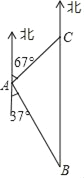
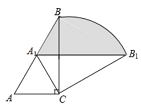
ЬтФПФкШн
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЕу
жаЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЕФБфЛЛЕу
ЕФБфЛЛЕу![]() ЕФзјБъЖЈвхШчЯТЃК
ЕФзјБъЖЈвхШчЯТЃК
ЕБ![]() ЪБЃЌЕу
ЪБЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌЕу
ЪБЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЕу![]() ЕФБфЛЛЕу
ЕФБфЛЛЕу![]() ЕФзјБъЪЧЁЁ ЁЁЃЛЕу
ЕФзјБъЪЧЁЁ ЁЁЃЛЕу![]() ЕФБфЛЛЕуЮЊ
ЕФБфЛЛЕуЮЊ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌдђ
ЃЌдђ![]() ЁЁ ЁЁЁуЃЛ
ЁЁ ЁЁЁуЃЛ
ЃЈ2ЃЉвбжЊХзЮяЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌ
ЃЌ![]() ЃЈЕу
ЃЈЕу![]() дкЕу
дкЕу![]() ЕФзѓВрЃЉЃЌЖЅЕуЮЊ
ЕФзѓВрЃЉЃЌЖЅЕуЮЊ![]() ЃЎЕу
ЃЎЕу![]() дкХзЮяЯп
дкХзЮяЯпЩЯЃЌЕу
![]() ЕФБфЛЛЕуЮЊ
ЕФБфЛЛЕуЮЊ![]() ЃЎШєЕу
ЃЎШєЕу![]() ЧЁКУдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧвЫФБпаЮ
ЧЁКУдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧвЫФБпаЮ![]() ЪЧСтаЮЃЌЧѓ
ЪЧСтаЮЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉШєЕу![]() ЪЧКЏЪ§
ЪЧКЏЪ§![]() ЭМЯѓЩЯЕФвЛЕуЃЌЕу
ЭМЯѓЩЯЕФвЛЕуЃЌЕу![]() ЕФБфЛЛЕуЮЊ
ЕФБфЛЛЕуЮЊ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌвд
ЃЌвд![]() ЮЊжБОЖзї
ЮЊжБОЖзї![]() ЃЌ
ЃЌ![]() ЕФАыОЖЮЊ
ЕФАыОЖЮЊ![]() ЃЌЧыжБНгаДГі
ЃЌЧыжБНгаДГі![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
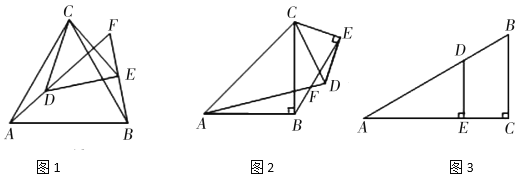
ЁОД№АИЁПЃЈ1ЃЉЃЈЉ3ЃЌ1ЃЉЃЛ90ЁуЃЛЃЈ2ЃЉ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЕФШЁжЕЗЖЮЇЪЧ
ЕФШЁжЕЗЖЮЇЪЧ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉвРОнЖдгІЕФЖЈвхПЩжБНгЕУЕу![]() ЁЂ
ЁЂ![]() ЕФзјБъЃЌШЛКѓвРОнЬтвтЛГіЭМаЮЃЌЙ§Еу
ЕФзјБъЃЌШЛКѓвРОнЬтвтЛГіЭМаЮЃЌЙ§Еу![]() зї
зї![]() жсЃЌДЙзуЮЊ
жсЃЌДЙзуЮЊ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() жсЃЌДЙзуЮЊ
жсЃЌДЙзуЮЊ![]() ЃЎНгЯТРДжЄУї
ЃЎНгЯТРДжЄУї![]() .гЩШЋЕШШ§НЧаЮЕФаджЪЕУЕН
.гЩШЋЕШШ§НЧаЮЕФаджЪЕУЕН![]() ЃЌШЛКѓПЩЧѓЕУ
ЃЌШЛКѓПЩЧѓЕУ![]() .
.
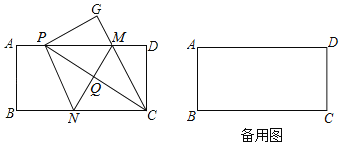
ЃЈ2ЃЉХзЮяЯп![]() ЕФЖЅЕуEЕФзјБъЮЊEЃЈ-2ЃЌmЃЉЃЌm>0ЃЌЩшЕуPЕФзјБъЮЊ
ЕФЖЅЕуEЕФзјБъЮЊEЃЈ-2ЃЌmЃЉЃЌm>0ЃЌЩшЕуPЕФзјБъЮЊ
![]() ЃЌЂйШє
ЃЌЂйШє![]() ЃЌдђЕу
ЃЌдђЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ШЛКѓвРОнЕу![]() ЧЁКУдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧвЫФБпаЮ
ЧЁКУдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧвЫФБпаЮ![]() ЪЧСтаЮЃЌПЩЕУЕНЙигкxКЭmЕФЗНГЬзщЃЌДгЖјПЩЧѓЕУmЕФжЕЃЛЂкШє
ЪЧСтаЮЃЌПЩЕУЕНЙигкxКЭmЕФЗНГЬзщЃЌДгЖјПЩЧѓЕУmЕФжЕЃЛЂкШє![]() ЃЌдђЕу
ЃЌдђЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎЭЌРэПЩСаГіЙигкxЁЂmЕФЗНГЬзщЃЌДгЖјЧѓЕУmЕФжЕЃЛ
ЃЎЭЌРэПЩСаГіЙигкxЁЂmЕФЗНГЬзщЃЌДгЖјЧѓЕУmЕФжЕЃЛ
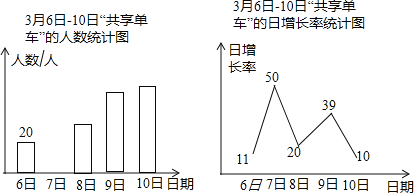
ЃЈ3ЃЉЩшЕуFЕФзјБъЮЊ![]() ЃЌвРОнЬтвтПЩЕУЕНЕу
ЃЌвРОнЬтвтПЩЕУЕНЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌШЛКѓвРОнСНЕуМфЕФОрРыЙЋЪНПЩЕУЕН
ЃЌШЛКѓвРОнСНЕуМфЕФОрРыЙЋЪНПЩЕУЕН![]() ЕФГЄЖШгыxЕФКЏЪ§ЙиЯЕЪНЃЌДгЖјПЩЧѓЕУ
ЕФГЄЖШгыxЕФКЏЪ§ЙиЯЕЪНЃЌДгЖјПЩЧѓЕУ![]() ЕФШЁжЕЗЖЮЇЃЌШЛКѓПЩЧѓЕУrЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇЃЌШЛКѓПЩЧѓЕУrЕФШЁжЕЗЖЮЇ.
ЃЈ1ЃЉЁпЕу![]() ЃЌ3ЃО1ЃЌ
ЃЌ3ЃО1ЃЌ
ЁрЕу![]() ЕФЖдгІЕу
ЕФЖдгІЕу![]() ЕФзјБъЪЧЃЈЉ3ЃЌ1ЃЉЃЎ
ЕФзјБъЪЧЃЈЉ3ЃЌ1ЃЉЃЎ
Ёп![]() ЃЌЉ4ЃМ2ЃЌ
ЃЌЉ4ЃМ2ЃЌ
ЁрЕу![]() ЕФБфЛЛЕуЮЊ
ЕФБфЛЛЕуЮЊ![]() ЕФзјБъЮЊЃЈЉ2ЃЌЉ4ЃЉЃЎ
ЕФзјБъЮЊЃЈЉ2ЃЌЉ4ЃЉЃЎ
Й§Еу![]() зї
зї![]() жсЃЌДЙзуЮЊ
жсЃЌДЙзуЮЊ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() жсЃЌДЙзуЮЊ
жсЃЌДЙзуЮЊ![]() ЃЎ
ЃЎ
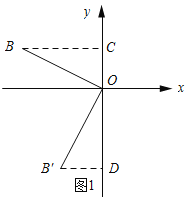
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
дк![]() КЭ
КЭ![]() жа
жа ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
Ёр![]() ЃЎ
ЃЎ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
Ёр![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊЃКЃЈЉ3ЃЌ1ЃЉЃЛ90ЁуЃЎ
ЃЈ2ЃЉгЩЬтвтЕУ![]() ЕФЖЅЕу
ЕФЖЅЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ЁпЕу![]() дкХзЮяЯп
дкХзЮяЯп![]() ЩЯЃЌ
ЩЯЃЌ
ЁрЩшЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ЂйШє![]() ЃЌдђЕу
ЃЌдђЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ЁпЕу![]() ЧЁКУдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧвЫФБпаЮ
ЧЁКУдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧвЫФБпаЮ![]() ЪЧСтаЮЃЌ
ЪЧСтаЮЃЌ
Ёр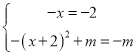
Ёр![]() ЃЌЗћКЯЬтвтЁЃ
ЃЌЗћКЯЬтвтЁЃ
ЂкШє![]() ЃЌдђЕу
ЃЌдђЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ЁпЕу![]() ЧЁКУдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧвЫФБпаЮ
ЧЁКУдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧвЫФБпаЮ![]() ЪЧСтаЮЃЌ
ЪЧСтаЮЃЌ
Ёр
Ёр![]() Лђ
Лђ![]() ЃЌЗћКЯЬтвтЃЎ
ЃЌЗћКЯЬтвтЃЎ
злЩЯЫљЪіЃЌ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉЩшЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ЕБ![]() ЪБЃЌНтЕУЃК
ЪБЃЌНтЕУЃК![]() ЃЌВЛКЯЬтвтЃЎ
ЃЌВЛКЯЬтвтЃЎ
ЕБ![]() ЪБЃЌНтЕУЃК
ЪБЃЌНтЕУЃК![]() ЃЌЗћКЯЬтвтЃЎ
ЃЌЗћКЯЬтвтЃЎ
ЁпЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЧв
ЃЌЧв![]() ЃЌ
ЃЌ
ЁрЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
Ёр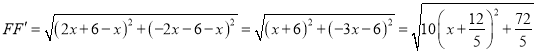 ЃЎ
ЃЎ
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() газюаЁжЕЃЌ
газюаЁжЕЃЌ![]() ЕФзюаЁжЕ
ЕФзюаЁжЕ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() газюДѓжЕЃЌ
газюДѓжЕЃЌ![]() ЕФзюДѓжЕ
ЕФзюДѓжЕ![]() ЃЎ
ЃЎ
Ёр![]() ЕФШЁжЕЗЖЮЇЮЊЃК
ЕФШЁжЕЗЖЮЇЮЊЃК![]() ЃЎ
ЃЎ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЕФШЁжЕЗЖЮЇЪЧ
ЕФШЁжЕЗЖЮЇЪЧ![]() ЃЎ
ЃЎ