题目内容
在菱形ABCD中，对角线AC、BD相交于点O．如果AC=8，BD=6，那么菱形的周长是________，菱形的面积是________．
20 24
分析：根据菱形的对角线可以求得菱形ABCD的面积，根据菱形对角线互相垂直平分的性质，可以求得BO=OD，AO=OC，在Rt△AOD中，根据勾股定理可以求得AB的长，即可求菱形ABCD的周长．
解答：
解：解：菱形的对角线为6、8，
则菱形的面积为
×6×8=24，
菱形对角线互相垂直平分，
∴BO=OD=3，AO=OC=4，
∴AB=
=5，
故菱形的周长为20，
答：菱形的周长为20，面积为24．故答案为：20；24．
点评：本题考查了菱形面积的计算，考查了勾股定理在直角三角形中的运用，考查了菱形各边长相等的性质，本题中根据勾股定理计算AB的长是解题的关键．
分析：根据菱形的对角线可以求得菱形ABCD的面积，根据菱形对角线互相垂直平分的性质，可以求得BO=OD，AO=OC，在Rt△AOD中，根据勾股定理可以求得AB的长，即可求菱形ABCD的周长．
解答：
解：解：菱形的对角线为6、8，则菱形的面积为
×6×8=24，菱形对角线互相垂直平分，
∴BO=OD=3，AO=OC=4，
∴AB=
=5，故菱形的周长为20，
答：菱形的周长为20，面积为24．故答案为：20；24．
点评：本题考查了菱形面积的计算，考查了勾股定理在直角三角形中的运用，考查了菱形各边长相等的性质，本题中根据勾股定理计算AB的长是解题的关键．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
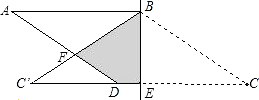如图，在菱形ABCD中，BE⊥CD于点E，AB=5，BE=3，把菱形沿着BE对折，使点C落在点C′处，则重叠部分（即阴影部分）的面积是
（2012•玉林）如图，在菱形ABCD中，对角线AC，BD相交于点O，且AC≠BD，则图中全等三角形有（ ）
（2012•百色）如图，在菱形ABCD中，E、F是对角线AC上的两点，且AE=CF．
