题目内容

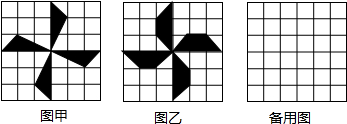
在边长为a的正方形纸片中剪去一个边长为b的小正方形（a＞b）（如图（1）），把余下的部分沿虚线剪开，拼成一个矩形（如图（2）），分别计算这两个图形阴影部分的面积，可以验证的乘法公式是______．（用字母表示）

解：在图1中，大正方形面积为a²，小正方形面积为b²，所以阴影部分的面积为a²-b²，
在图2中，阴影部分为一长方形，长为a+b，宽为a-b，则面积为（a+b）（a-b），
由于两个阴影部分面积相等，所以有a²-b²=（a+b）（a-b）成立．
故本题答案为：a²-b²=（a+b）（a-b）或（a+b）（a-b）=a²-b²．
分析：分别表示出两种情况下的阴影部分的面积，而面积是相等的，故可得到结果．
点评：本题考查了平方差公式几何意义的理解，将整式运算与几何图形结合，注意各个量的变化．

练习册系列答案

江苏5年经典系列答案

初中毕业学业考试指导丛书系列答案

芒果教辅小学数学应用题系列答案

春雨教育小学数学图解巧练应用题系列答案

龙门书局系列答案

学而思小学数学秘籍系列答案

学林教育小学数学图解应用题系列答案

金博优题典单元练测活页卷系列答案

DIY英语系列答案

晨光全优口算应用题天天练系列答案

相关题目

贝贝和京京玩掷飞镖游戏，他们先在墙上挂了如图1的纸靶，靶中两个正方形的边长分别为5cm和10cm，蒙上眼在一定距离外投掷飞镖，掷中阴影部分为贝贝胜，否则京京胜，未掷中靶面或掷中分界线不算．如果你是裁判：
（1）你认为游戏公平吗？为什么？
（2）贝贝和京京更换了纸靶（如图2），在边长为10cm的正方形纸靶中央是一个不规则图形，游戏方法不变，他们游戏的结果记录如下表：

游戏次数	50	100	150	200	300	500	1000
贝贝胜	22	54	74	109	162	258	522
京京胜	28	46	76	91	138	242	478
京京获胜的频率	0.56	0.46	0.503	0.455	0.47	0.482	m

请写出表格中m的值（精确到0.01）；然后利用表中数据估算出纸靶中央不规则图形的面积并说明理由．

如图所示，在一个边长为2cm的正方形纸片中，剪去一个边长为2cm的等边三角形，求出图中阴影部分的面积．（取

在数学活动课上，李老师要求同学们在边长为1的正方形格纸中，画出一个“风车”图案．
小红同学的做法是：如图甲所示，把一个三角形按顺时针方向旋转90°，连续转三次，形成四个叶片的“风车”图案；类似地，把一个梯形按顺时针方向旋转90°，连续转三次，形成图乙所示的四个叶片的“风车”图案．
请你仿照小红同学的做法，在备用图中，画一个新的四个叶片的“风车”图案，并使得“风车”的四个叶片的面积与图乙的四个叶片的面积相同．

贝贝和京京玩掷飞镖游戏，他们先在墙上挂了如图1的纸靶，靶中两个正方形的边长分别为5cm和10cm，蒙上眼在一定距离外投掷飞镖，掷中阴影部分为贝贝胜，否则京京胜，未掷中靶面或掷中分界线不算．如果你是裁判：
（1）你认为游戏公平吗？为什么？
（2）贝贝和京京更换了纸靶（如图2），在边长为10cm的正方形纸靶中央是一个不规则图形，游戏方法不变，他们游戏的结果记录如下表：
游戏次数 50 100 150 200 300 500 1000
贝贝胜 22 54 74 109 162 258 522
京京胜 28 46 76 91 138 242 478
京京获胜的频率 0.56 0.46 0.503 0.455 0.47 0.482 m
请写出表格中m的值（精确到0.01）；然后利用表中数据估算出纸靶中央不规则图形的面积并说明理由．

贝贝和京京玩掷飞镖游戏，他们先在墙上挂了如图1的纸靶，靶中两个正方形的边长分别为5cm和10cm，蒙上眼在一定距离外投掷飞镖，掷中阴影部分为贝贝胜，否则京京胜，未掷中靶面或掷中分界线不算．如果你是裁判：
（1）你认为游戏公平吗？为什么？
（2）贝贝和京京更换了纸靶（如图2），在边长为10cm的正方形纸靶中央是一个不规则图形，游戏方法不变，他们游戏的结果记录如下表：

游戏次数	50	100	150	200	300	500	1000
贝贝胜	22	54	74	109	162	258	522
京京胜	28	46	76	91	138	242	478
京京获胜的频率	0.56	0.46	0.503	0.455	0.47	0.482	m

请写出表格中m的值（精确到0.01）；然后利用表中数据估算出纸靶中央不规则图形的面积并说明理由．