题目内容
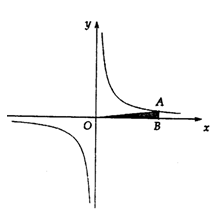
 如图,已知点A在反比例函数的图象上,AB⊥x轴于点B,点C(0,1),若△ABC的面积是3,则反比例函数的解析式为________.
如图,已知点A在反比例函数的图象上,AB⊥x轴于点B,点C(0,1),若△ABC的面积是3,则反比例函数的解析式为________.

分析:设A点坐标为(a,b),反比例函数的解析式为y=
 ,利用S△ABC=S梯形ABOC-S△BOC,即可得到ab=6,然后把A(a,b)代入反比例函数的解析式为y=
,利用S△ABC=S梯形ABOC-S△BOC,即可得到ab=6,然后把A(a,b)代入反比例函数的解析式为y= ,得求出k的值.
,得求出k的值.解答:设A点坐标为(a,b),反比例函数的解析式为y=
 ,则OB=a,AB=b,
,则OB=a,AB=b,∵S△ABC=S梯形ABOC-S△BOC,即
 (OC+AB)•OB-
(OC+AB)•OB- OC•OB=3,
OC•OB=3,∴
 •(1+b)•a-
•(1+b)•a- •1•a=3,
•1•a=3,∴ab=6,
把A(a,b)代入反比例函数的解析式为y=
 ,得k=ab=6,
,得k=ab=6,∴反比例函数的解析式为 y=
 .
.故答案为y=
 .
.点评:本题考查了反比例函数y=
 (k≠0)图象上点的横纵坐标的特点:横纵坐标的积为定值k.也考查了平面直角坐标系中不规则的几何图形的面积的计算方法.
(k≠0)图象上点的横纵坐标的特点:横纵坐标的积为定值k.也考查了平面直角坐标系中不规则的几何图形的面积的计算方法. 
练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目


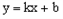 的图象与反比例函数
的图象与反比例函数 的图象相交于A、B两点。
的图象相交于A、B两点。 在一次函数的图象上,点
在一次函数的图象上,点 在反比函数的图象上。当
在反比函数的图象上。当 时,直接写出m的取值范围。
时,直接写出m的取值范围。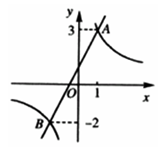
 的图象相交于A、B两点。
的图象相交于A、B两点。
 的图象经过点A(3,m),过点A作
的图象经过点A(3,m),过点A作 轴于点B,
轴于点B, 的面积为
的面积为
 的图象上,求当
的图象上,求当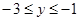 时,对应的x的取值范围;
时,对应的x的取值范围;