题目内容
7.(1)计算:($\sqrt{5}$)2-$\root{3}{-8}$-|-3|+(-$\frac{1}{5}$)0;(2)已知:$\frac{1}{3}$(x+2)2-3=0,求x.
分析 (1)原式利用平方根、立方根定义,绝对值的代数意义,以及零指数幂法则计算即可得到结果;
(2)方程整理后,利用平方根定义开方即可求出x的值.
解答 解:(1)原式=5+2-3+1=5;
(2)方程整理得:(x+2)2=9,
开方得:x+2=3或x+2=-3,
解得:x=1或x=-5.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
18.使二次根式$\sqrt{x-2}$有意义的x的取值范围是( )
| A. | x>0 | B. | x>2 | C. | x≥2 | D. | x≠2 |
15.计算2a2b-3a2b的正确结果是( )
| A. | ab2 | B. | -ab2 | C. | a2b | D. | -a2b |
19.不等式组$\left\{\begin{array}{l}{1-x<2}\\{2x≤6}\end{array}\right.$的解集为( )
| A. | x>-1 | B. | x≤3 | C. | 1<x≤3 | D. | -1<x≤3 |
16.在墙壁上用两个钉子就能固定一根横放的木条,这样做根据的道理是( )
| A. | 两点确定一条直线 | B. | 两点确定一条线段 | ||
| C. | 两点之间,直线最短 | D. | 两点之间,线段最短 |
17.已知x=y,字母m可以取任意有理数,下列等式不一定成立的是( )
| A. | x+m=y+m | B. | x-m=y-m | C. | xm=ym | D. | x+m=x-m |
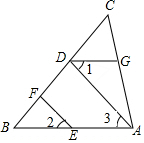 如图,EF⊥BC,AD⊥BC,∠1=∠2,∠B=30°.求∠GDB的度数.
如图,EF⊥BC,AD⊥BC,∠1=∠2,∠B=30°.求∠GDB的度数.