Question

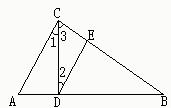10、如图，已知AC⊥BC，CD⊥AB，∠1=∠2，下面七个结论中正确的有（　　）
①∠A=∠B；②∠A=∠3；③AC∥DE；④∠2与∠B互为余角；⑤点D到CB的垂线段是线段CE；⑥在CA、CB、CD三条线段中，CD最短；⑦线段CD是点C到AB的距离．

A、2个

B、3个

C、4个

D、5个

Answer 1

分析：根据已知条件和观察图形，结合余角的性质、垂直的定义、垂线的性质和点到直线的距离进行判断，做出正确选择．

解答：解：由题意知，
①∠A与∠B互余，所以错误；
②根据同角的余角相等，得∠A=∠3，所以正确；
③∵∠1=∠2，∴AC∥DE，所以正确；
④根据同角的余角相等，得∠2=∠B，所以错误；
⑤点D到CB的垂线段是线段DE，所以错误；
⑥根据垂线段最短，知在CA、CB、CD三条线段中，CD最短，所以正确；
⑦线段CD的长度是点C到AB的距离，所以错误．
正确的有②③⑥，共3个．
故选B．

点评：本题考查了垂直的定义、余角的性质、垂线的性质和点到直线的距离，要注意领会由垂直得直角这一要点．