题目内容
 如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1与∠2互补,判断HF与AB是否垂直,并说明理由.
如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1与∠2互补,判断HF与AB是否垂直,并说明理由.分析:根据AC⊥BC,DE⊥AC,易证DE∥BC,于是∠1=∠3,而∠1与∠2互补,那么∠2+∠3=180°,从而可证FH∥CD,结合CD⊥AB,易得∠HFD=90°,即HF⊥AB.
解答: 解:垂直.理由如下:
解:垂直.理由如下:
∵∠1与∠2互补,
∴∠1+∠2=180°,
∵DE⊥AC,AC⊥BC,
∴∠ADE=∠ACB=90°,
∴DE∥BC,
∴∠1=∠3,
∴∠2+∠3=180°,
∴FH∥CD,
∴∠HFD=∠BDC=90°,
又∵CD⊥AB,
∴∠BDC=90°,
∴∠HFD=90°,
∴HF⊥AB.
 解:垂直.理由如下:
解:垂直.理由如下:∵∠1与∠2互补,
∴∠1+∠2=180°,
∵DE⊥AC,AC⊥BC,
∴∠ADE=∠ACB=90°,
∴DE∥BC,
∴∠1=∠3,
∴∠2+∠3=180°,
∴FH∥CD,
∴∠HFD=∠BDC=90°,
又∵CD⊥AB,
∴∠BDC=90°,
∴∠HFD=90°,
∴HF⊥AB.
点评:本题考查了平行线的性质和判定,解题的关键是证明∠1=∠3.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
 19、如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1+∠2=180°,要证HF⊥AB,请完善证明过程,并在括号内填上相应依据:
19、如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1+∠2=180°,要证HF⊥AB,请完善证明过程,并在括号内填上相应依据: (2012•肇庆)如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.
(2012•肇庆)如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD. 如图,已知AC=BC,∠1=∠2,点D、E分别在CA、CB的延长线上.
如图,已知AC=BC,∠1=∠2,点D、E分别在CA、CB的延长线上.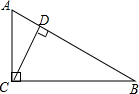 如图,已知AC⊥BC,CD⊥AB于点D,AC=5cm,BC=12cm,AB=13cm,那么点B到AC的距离是
如图,已知AC⊥BC,CD⊥AB于点D,AC=5cm,BC=12cm,AB=13cm,那么点B到AC的距离是