题目内容
如果(a2+b2)(a2+b2-1)=20,那么a2+b2= .
考点:换元法解一元二次方程
专题:
分析:先设y=a2+b2,则原方程变形为y2-y-20=0,运用因式分解法解得y1=-4,y2=5,从而求得a2+b2的值.
解答:解:设y=a2+b2,
原方程变形为y2-y-20=0,
(y+4)(y-5)=0,
解得y1=-4,y2=5,
因为a2、b2是非负数,
所以a2+b2=5.
故答案为5.
原方程变形为y2-y-20=0,
(y+4)(y-5)=0,
解得y1=-4,y2=5,
因为a2、b2是非负数,
所以a2+b2=5.
故答案为5.
点评:本题考查了换元法解一元二次方程:我们常用的是整体换元法,是在已知或者未知中,某个代数式几次出现,而用一个字母来代替它从而简化问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
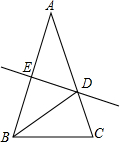 如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论:①BD平分∠ABC;②AD=BD=BC;③△BDC的周长等于AB+BC;④D是AC中点.其中正确的命题序号是( )
如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论:①BD平分∠ABC;②AD=BD=BC;③△BDC的周长等于AB+BC;④D是AC中点.其中正确的命题序号是( )| A、①②③ | B、①②④ |
| C、②③④ | D、①③④ |
下列运算正确的是( )
| A、-22=4 | ||||
B、(-
| ||||
C、(-
| ||||
| D、(-2)3=-6 |
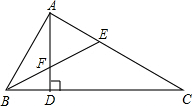 如图所示,∠BAC=90°,AD⊥BC,垂足为D,BE平分∠ABC,交AC于E,交AD于F,试判断△AEF的形状,并说明理由.
如图所示,∠BAC=90°,AD⊥BC,垂足为D,BE平分∠ABC,交AC于E,交AD于F,试判断△AEF的形状,并说明理由.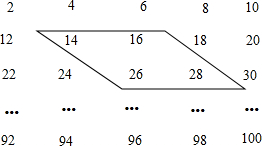 下列数阵是由50个偶数排成的.
下列数阵是由50个偶数排成的.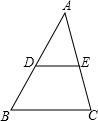 如图,在△ABC中,点D、E分别是AB、AC的中点,则下列结论:
如图,在△ABC中,点D、E分别是AB、AC的中点,则下列结论: