题目内容
【题目】 如图，点E在△DBC的边DB上，点A在△DBC内部，∠DAE=∠BAC=90°，AD=AE，AB=AC．给出下列结论：①BD=CE；②BC=DC；③∠ABD+∠ECB=45°；④BD⊥CE．其中正确的结论是（ ）
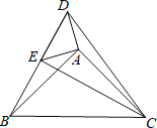
A.①②③④B.②④C.①②③D.①③④
【答案】D
【解析】
根据等腰直角三角形的性质，全等三角形的判定与性质逐一判断即可．
解：∵∠DAE=∠BAC=90°，AD=AE，AB=AC，
∴∠DAE+∠EAB=∠BAC+∠EAB，
∴∠DAB=∠AEC，
∴△AEC≌△DAE（SAS），
∴BD=CE，
①正确；
∵∠DBA=∠ACE，
∴∠ABD+∠ECB=45°；
③正确；
∵∠AEC=∠BDA=45°，
∴∠DEC=90°，
∴BD⊥CE，
∴④正确；
BC与DC不能判断是否相等，故②错误；
故选：D．
练习册系列答案
名校课堂系列答案
相关题目
【题目】某公司共有
三个部门，根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图．
各部门人数及每人所创年利润统计表
部门 | 员工人数 | 每人所创的年利润/万元 |
A | 5 | 10 |
B |
| 8 |
C |
| 5 |
（1）①在扇形图中，C部门所对应的圆心角的度数为___________；
②在统计表中，
___________，
___________；
（2）求这个公司平均每人所创年利润．
