题目内容
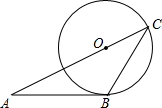（2012•泰安）如图，AB与⊙O相切于点B，AO的延长线交⊙O于点C，连接BC，若∠ABC=120°，OC=3，则 |
| BC |
分析：连接OB，由于AB是切线，那么∠ABO=90°，而∠ABC=120°，易求∠OBC，而OB=OC，那么∠OBC=∠OCB，进而求出∠BOC的度数，再利用弧长公式即可求出
的长．
|
| BC |
解答：
解：连接OB，
∵AB与⊙O相切于点B，
∴∠ABO=90°，
∵∠ABC=120°，
∴∠OBC=30°，
∵OB=OC，
∴∠OCB=30°，
∴∠BOC=120°，
∴
的长为
=
=2π，
故选B．
解：连接OB，∵AB与⊙O相切于点B，
∴∠ABO=90°，
∵∠ABC=120°，
∴∠OBC=30°，
∵OB=OC，
∴∠OCB=30°，
∴∠BOC=120°，
∴
|
| BC |
| nπr |
| 180 |
| 120×π×3 |
| 180 |
故选B．
点评：本题考查了切线的性质、弧长公式，解题的关键是连接OB，构造直角三角形．
练习册系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
（2012•泰安）如图，AB是⊙O的直径，弦CD⊥AB，垂足为M，下列结论不成立的是（ ）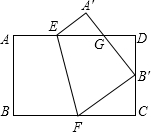
（2012•泰安）如图，将矩形纸片ABCD沿EF折叠，使点B与CD的中点重合，若AB=2，BC=3，则△FCB′与△B′DG的面积之比为（ ）
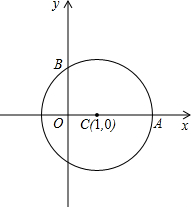（2012•泰安）如图，半径为2的⊙C与x轴的正半轴交于点A，与y轴的正半轴交于点B，点C的坐标为（1，0）．若抛物线y=-
（2012•泰安）如图，AB∥CD，E，F分别为AC，BD的中点，若AB=5，CD=3，则EF的长是（ ）