题目内容
(1998•黄冈)已知关于x的方程k2x2+(2k-1)x+1=0有两个不相等的实数根x1、x2.
(1)求k的取值范围;
(2)当k为何值时,x1与x2互为倒数.
解:(1)依题意,有△>0,即(2k-1)2-4k2>0.解得k<
.∴k的取值范围是k<
.
(2)依题意,得
∴当k=1或k=-1时,x1与x2互为倒数.
上面解答有无错误?若有,指出错误之处,并直接写出正确答案.
(1)求k的取值范围;
(2)当k为何值时,x1与x2互为倒数.
解:(1)依题意,有△>0,即(2k-1)2-4k2>0.解得k<
| 1 |
| 4 |
| 1 |
| 4 |
(2)依题意,得
|
∴当k=1或k=-1时,x1与x2互为倒数.
上面解答有无错误?若有,指出错误之处,并直接写出正确答案.
分析:(1)先根据有两个不相等的实数根x1、x2,得出(2k-1)2-4k2>0,求出k的取值范围,再根据k≠0,即可得出答案.
(2)先根据x1与x2互为倒数得出
,求出k的值,再根据k<
,即可得出答案.
(2)先根据x1与x2互为倒数得出
|
| 1 |
| 4 |
解答:解:(1)错误:
根据题意得:,
有△>0,即(2k-1)2-4k2>0.
解得k<
,
∵k≠0,
∴k的取值范围是k<
且k≠0.
(2)依题意,得
解得:k=1或k=-1,
∵k<
,
∴k=-1时,x1与x2互为倒数.
根据题意得:,
有△>0,即(2k-1)2-4k2>0.
解得k<
| 1 |
| 4 |
∵k≠0,
∴k的取值范围是k<
| 1 |
| 4 |
(2)依题意,得
|
解得:k=1或k=-1,
∵k<
| 1 |
| 4 |
∴k=-1时,x1与x2互为倒数.
点评:此题考查了一元二次方程根的判别式、根与系数的关系,一元二次方程根的情况与判别式△的关系:△>0?方程有两个不相等的实数根;△=0?方程有两个相等的实数根;△<0?方程没有实数根.

练习册系列答案
相关题目
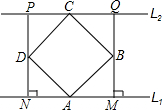 (1998•黄冈)如图,已知四边形ABCD是正方形,分别过A、C两点作l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB、ND分别交l2于Q、P.求证:四边形PQMN是正方形.
(1998•黄冈)如图,已知四边形ABCD是正方形,分别过A、C两点作l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB、ND分别交l2于Q、P.求证:四边形PQMN是正方形.