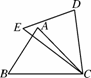
题目内容
如图5316,在△ABC中,以AB为直径的⊙O交AC于点D,∠DBC=∠BAC.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为2,∠BAC=30°,求图中阴影部分的面积.
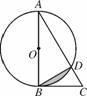
(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°.∴∠ABD+∠BAC=90°.
∵∠DBC=∠BAC,∴∠ABD+∠DBC=90°.
∴BC是⊙O的切线.
(2)解:连接OD,∵∠BAC=30°,∴∠BOD=60°.
∵OB=OD,∴△OBD是等边三角形.
∴S阴影=S扇形OBD-S△OBD= -
-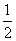 ×2×
×2× =
= -
- .
.

练习册系列答案
相关题目
 ,圆心距为
,圆心距为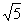 ,则两圆的位置关系为 ( )
,则两圆的位置关系为 ( )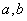 ,即
,即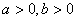 ,有下面的不等式:
,有下面的不等式: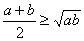 当且仅当
当且仅当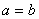 时取到等号
时取到等号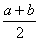 叫做正数
叫做正数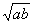 叫做正数
叫做正数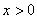 ,求函数
,求函数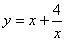 的最小值。
的最小值。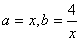 ,则有
,则有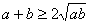 ,得
,得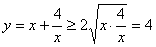 ,当且仅当
,当且仅当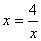 时,即
时,即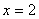 时,函数有最小值,最小值为
时,函数有最小值,最小值为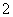 。
。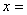 时,函数
时,函数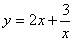 取到最小值,最小值
取到最小值,最小值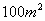 的矩形花园,问这个矩形的长、宽各为多
的矩形花园,问这个矩形的长、宽各为多 少时,所
少时,所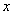 取何值时,函数
取何值时,函数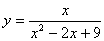 取到最大值,最大值为多少?
取到最大值,最大值为多少?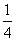 π B.π-
π B.π-


 r B.
r B. r C.r D.2r
r C.r D.2r