Question

【题目】如图①，直线AB的解析式为y＝﹣x+4，抛物线y＝﹣+bx+c与y轴交于点A，与x轴交于点C（6，0），点P是抛物线上一动点，设点P的横坐标为m．

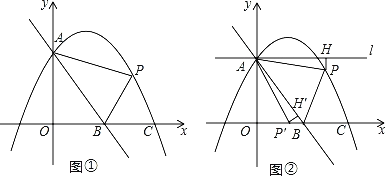
（1）求抛物线的解析式；

（2）当点P在第一象限内时，求△ABP面积的最大值，并求此时点P的坐标；

（3）如图②，当点P在y轴右侧时，过点A作直线l∥x轴，过点P作PH⊥l于点H，将△APH绕点A顺时针旋转，当点H的对应点H′恰好落在直线AB上时，点P的对应点P′恰好落在坐标轴上，请直接写出点P的横坐标．

Answer 1

【答案】（1）；（2）面积最大值为8，；（3）或

【解析】

（1）先利用直线进行确定则A（0，4），然后利用待定系数法求抛物线解析式；

（2）连接OP，设P（m，﹣m2+m+4），解方程﹣x+4＝0得B（3，0），根据三角形面积公式，利用面积的和差得到S△ABP＝S△AOP+S△POB﹣S△AOB＝×4m+×3（﹣m2+m+4）﹣×3×4，然后根据二次函数的性质解决问题；

（3）先利用勾股定理计算出AB＝5，讨论：当点P′落在x轴上，如图2，根据旋转的性质得＝4﹣（﹣m2+m+4）＝m2﹣m，AH′＝AH＝m，∠P′H′A＝∠PHA＝90°，再证明△BP′H′∽△BAO，利用相似得到BH′＝m2﹣m，然后利用AH′+BH′＝AB得到m+m2﹣m＝5，解方程求出m即可得到P点横坐标；当点P′落在y轴上，如图3，同理可得P′H′＝PH＝m2﹣m，AH′＝AH＝m，∠P′H′A＝∠PHA＝90°，通过证明△AH′P′′∽△AOB，然后利用相似比得到（m2﹣m）：3＝m：4，然后解关于m的方程即可得到对应P点横坐标．

解：（1）当x＝0时，y＝﹣x+4＝4，则A（0，4），

∵抛物线y＝﹣x2+bx+c与y轴交于点A，与x轴交于点C（6，0），

∴，解得：，

∴抛物线解析式为y＝﹣x2+x+4；

（2）连接OP，

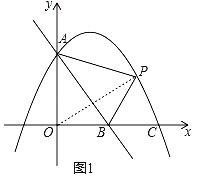
设P（m，﹣m2+m+4），

当y＝0时，﹣x+4＝0，解得x＝3，

则B（3，0），

∵S△ABP＝S△AOP+S△POB﹣S△AOB＝×4m+×3（﹣m2+m+4）﹣×3×4

＝﹣m2+4m，

＝﹣（m﹣4）2+8，

当m＝4时，△ABP面积有最大值，最大值为8，此时P点坐标为（4，4）；

（3）在Rt△OAB中，AB＝＝＝5，

当点落在x轴上，如图2，

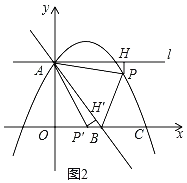
∵△APH绕点A顺时针旋转，使点H的对应点恰好落在直线AB上，同时恰好落在x轴上

∴＝PH＝4﹣（﹣m2+m+4）＝m2﹣m，＝AH＝m，＝∠PHA＝90°，

∵＝∠ABO，

∴∽△BAO，

∴：OA＝：OB，即（m2﹣m）：4＝：3，

∴＝m2﹣m，

∵，

∴m+m2﹣m＝5，

解得m1＝2，m2＝﹣2（舍去），

此时P点横坐标为2；

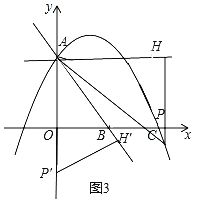
当点P′落在y轴上，如图3，

同理可得＝PH＝m2﹣m，＝AH＝m，＝∠PHA＝90°，

∵＝∠BAO，

∴∽△AOB，

∴：OB＝AH′：AO，即（m2﹣m）：3＝m：4，

整理得4m2﹣25m＝0，

解得m1＝，m2＝0（舍去），

此时P点横坐标为；

综上所述，P点横坐标为2或．