ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌАыдВOЕФжБОЖ![]() ЃЌдк
ЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌАыдВOвд
ЃЌАыдВOвд![]() ЕФЫйЖШДгзѓЯђгвдЫЖЏЃЌдкдЫЖЏЙ§ГЬжаЃЌЕуDЁЂEЪМжедкжБЯпBCЩЯЃЌЩшдЫЖЏЪБМфЮЊ
ЕФЫйЖШДгзѓЯђгвдЫЖЏЃЌдкдЫЖЏЙ§ГЬжаЃЌЕуDЁЂEЪМжедкжБЯпBCЩЯЃЌЩшдЫЖЏЪБМфЮЊ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌАыдВOдк
ЪБЃЌАыдВOдк![]() ЕФзѓВрЃЌ
ЕФзѓВрЃЌ![]() ЃЎ
ЃЎ
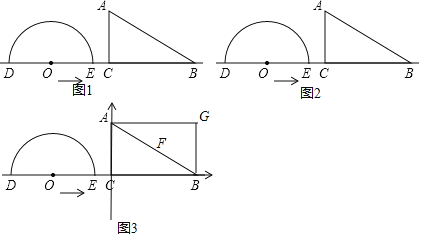
![]() ШчЭМ1ЕБ
ШчЭМ1ЕБ![]() ЪБЃЌдВаФOЕНABЫљдкжБЯпЕФОрРыЪЧ______cmЃЎ
ЪБЃЌдВаФOЕНABЫљдкжБЯпЕФОрРыЪЧ______cmЃЎ
![]() ЕБtЮЊКЮжЕЪБЃЌ
ЕБtЮЊКЮжЕЪБЃЌ![]() ЕФБпABЫљдкЕФжБЯпгыАыдВOЫљдкдВЯрЧаЃПЧѓЪБМфtЃЎ
ЕФБпABЫљдкЕФжБЯпгыАыдВOЫљдкдВЯрЧаЃПЧѓЪБМфtЃЎ
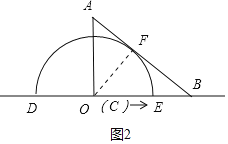
![]() ШчЭМ2ЃЌЯпЖЮABЕФжаЕуЮЊFЃЌЧѓдВаФOгыBЁЂFСНЕуЙЙГЩвдBFЮЊбќЕФЕШбќШ§НЧаЮЪБдЫЖЏЕФЪБМфtЃЎ
ШчЭМ2ЃЌЯпЖЮABЕФжаЕуЮЊFЃЌЧѓдВаФOгыBЁЂFСНЕуЙЙГЩвдBFЮЊбќЕФЕШбќШ§НЧаЮЪБдЫЖЏЕФЪБМфtЃЎ
![]() дкЭМ2ЕФЛљДЁЩЯЃЌНЈСЂШчЭМЫљЪОЕФЦНУцжБНЧзјБъЯЕЃЌЫФБпаЮACBGЪЧОиаЮЃЌШчЭМ3ЃЌАыдВOЯђгвдЫЖЏЕФЭЌЪБОиаЮвВЯђгвдЫЖЏЃЌЫйЖШЮЊ
дкЭМ2ЕФЛљДЁЩЯЃЌНЈСЂШчЭМЫљЪОЕФЦНУцжБНЧзјБъЯЕЃЌЫФБпаЮACBGЪЧОиаЮЃЌШчЭМ3ЃЌАыдВOЯђгвдЫЖЏЕФЭЌЪБОиаЮвВЯђгвдЫЖЏЃЌЫйЖШЮЊ![]() ЃЌЮЪОЙ§ЖрГЄЪБМфOЁЂFЁЂGдкЭЌвЛЬѕжБЯпЩЯЃЌЧѓЪБМф
ЃЌЮЪОЙ§ЖрГЄЪБМфOЁЂFЁЂGдкЭЌвЛЬѕжБЯпЩЯЃЌЧѓЪБМф![]() ВЂЧѓГіДЫЪБDGЕФжБЯпНтЮіЪНЃЎ
ВЂЧѓГіДЫЪБDGЕФжБЯпНтЮіЪНЃЎ
ЁОД№АИЁПЃЈ1ЃЉ9ЃЛЃЈ2ЃЉЕБ![]() Лђ32sЪБЃЌABгыАыдВOЫљдкЕФдВЯрЧаЃЛЃЈ3ЃЉТњзуЬѕМўЕФtЕФжЕЮЊ
Лђ32sЪБЃЌABгыАыдВOЫљдкЕФдВЯрЧаЃЛЃЈ3ЃЉТњзуЬѕМўЕФtЕФжЕЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ4ЃЉ
ЃЛЃЈ4ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
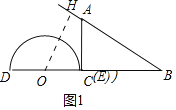
ЃЈ1ЃЉЕБt=2ЪБЃЌЕуEгыЕуCжиКЯЃЌШчЭМ1жаЃЌзїOHЁЭABгкHЃЎНтжБНЧШ§НЧаЮЧѓГіOHМДПЩЃЛ
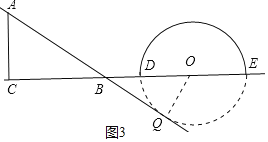
ЃЈ2ЃЉЗжСНжжЧщаЮЂйШчЭМ2жаЃЌЙ§CЕузїCFЁЭABЃЌНЛABгкFЕуЃЛЂкЕБЕуOдЫЖЏЕНBЕуЕФгвВрЃЌЧвOB=12cmЪБЃЌШчЭМ3жаЃЌЙ§ЕуOзїOQЁЭжБЯпABЃЌДЙзуЮЊQЃЎЗжБ№ЧѓНтМДПЩЃЛ
ЃЈ3ЃЉЂйЕБЕуOгыCжиКЯЪБЃЌЁїBOFЪЧЕШбќШ§НЧаЮЃЌДЫЪБt=8ЃЛЂкЕБBF=BOЪБЃЌдкRtЁїABCжаЃЌ![]() ЃЌЭЦГіBOЁф=4
ЃЌЭЦГіBOЁф=4![]() ЛђBOЁх=4
ЛђBOЁх=4![]() ЪБЃЌЁїOBFЪЧЕШбќШ§НЧаЮЃЌгЩДЫМДПЩНтОіЮЪЬтЃЛ
ЪБЃЌЁїOBFЪЧЕШбќШ§НЧаЮЃЌгЩДЫМДПЩНтОіЮЪЬтЃЛ
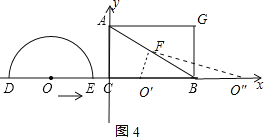
ЃЈ4ЃЉtУыКѓЃЌGЃЈ12+0.5tЃЌ4![]() ЃЉЃЌFЃЈ6+0.5tЃЌ2
ЃЉЃЌFЃЈ6+0.5tЃЌ2![]() ЃЉЃЌOЃЈ-8+tЃЌ0ЃЉЃЌЕБOЁЂFЁЂGЙВЯпЪБЃЌЕуFЪЧOЁЂGЕФжаЕуЃЌдђга
ЃЉЃЌOЃЈ-8+tЃЌ0ЃЉЃЌЕБOЁЂFЁЂGЙВЯпЪБЃЌЕуFЪЧOЁЂGЕФжаЕуЃЌдђга![]() =6+0.5tЃЌЧѓГіtМДПЩНтОіЮЪЬтЃЛ
=6+0.5tЃЌЧѓГіtМДПЩНтОіЮЪЬтЃЛ
НтЃК![]() ШчЭМ1жаЃЌзї
ШчЭМ1жаЃЌзї![]() гкHЃЎ
гкHЃЎ
ЕБ![]() ЪБЃЌЕуEгыЕуCжиКЯЃЌ
ЪБЃЌЕуEгыЕуCжиКЯЃЌ![]() ЃЌ
ЃЌ
дк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊ9ЃЎ
![]() ШчЭМ2жаЃЌЙ§CЕузї
ШчЭМ2жаЃЌЙ§CЕузї![]() ЃЌНЛABгкFЕуЃЛ
ЃЌНЛABгкFЕуЃЛ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЛ
ЃЛ
ЕБАыдВOгы![]() ЕФБпABЯрЧаЪБЃЌ
ЕФБпABЯрЧаЪБЃЌ
гж![]() дВаФOЕНABЕФОрРыЕШгк6cmЃЌ
дВаФOЕНABЕФОрРыЕШгк6cmЃЌ
ЧвдВаФOгждкжБЯпBCЩЯЃЌ
![]() гыCжиКЯЃЌ
гыCжиКЯЃЌ
МДЕБOЕудЫЖЏЕНCЕуЪБЃЌАыдВOгы![]() ЕФБпABЯрЧаЃЛ
ЕФБпABЯрЧаЃЛ
ДЫЪБЕуOдЫЖЏСЫ8cmЃЌЫљЧѓдЫЖЏЪБМфЮЊ![]() ЃЌ
ЃЌ
![]() ЕБЕуOдЫЖЏЕНBЕуЕФгвВрЃЌЧв
ЕБЕуOдЫЖЏЕНBЕуЕФгвВрЃЌЧв![]() ЪБЃЌШчЭМ3жаЃЌЙ§ЕуOзї
ЪБЃЌШчЭМ3жаЃЌЙ§ЕуOзї![]() жБЯпABЃЌДЙзуЮЊQЃЎ
жБЯпABЃЌДЙзуЮЊQЃЎ
дк![]() жаЃЌ
жаЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
МДOQгыАыдВOЫљдкЕФдВЯрЧа![]() ДЫЪБЕуOдЫЖЏСЫ32cmЃЎ
ДЫЪБЕуOдЫЖЏСЫ32cmЃЎ
ЫљЧѓдЫЖЏЪБМфЮЊЃК![]() ЃЌ
ЃЌ
злЩЯПЩжЊЕБ![]() Лђ32sЪБЃЌABгыАыдВOЫљдкЕФдВЯрЧаЃЛ
Лђ32sЪБЃЌABгыАыдВOЫљдкЕФдВЯрЧаЃЛ
![]() ШчЭМ4жаЃЌ
ШчЭМ4жаЃЌ
![]() ЕБЕуOгыCжиКЯЪБЃЌ
ЕБЕуOгыCжиКЯЪБЃЌ![]() ЪЧЕШбќШ§НЧаЮЃЌДЫЪБ
ЪЧЕШбќШ§НЧаЮЃЌДЫЪБ![]() ЃЛ
ЃЛ
![]() ЕБ
ЕБ![]() ЪБЃЌдк
ЪБЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ
![]() Лђ
Лђ![]() ЪБЃЌ
ЪБЃЌ![]() ЪЧЕШбќШ§НЧаЮЃЌ
ЪЧЕШбќШ§НЧаЮЃЌ
ДЫЪБ![]() Лђ
Лђ![]()
злЩЯЫљЪіЃЌТњзуЬѕМўЕФtЕФжЕЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
![]() УыКѓЃЌ
УыКѓЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЕБOЁЂFЁЂGЙВЯпЪБЃЌЕуFЪЧOЁЂGЕФжаЕуЃЌ
дђга![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ДЫЪБ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЩшжБЯпDGЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
дђ![]() ЃЌНтЕУ
ЃЌНтЕУ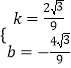
![]() ЃЎ
ЃЎ