题目内容
如图,在△ABD和△FEC中,点B,C,D,E在同一直线上,且AB=FE,BC=DE,∠B=∠E.求证:∠ADB=∠FCE.

【考点】全等三角形的判定与性质.
【专题】证明题.
【分析】根据等式的性质得出BD=CE,再利用SAS得出:△ABD与△FEC全等,进而得出∠ADB=∠FCE.
【解答】证明:∵BC=DE,
∴BC+CD=DE+CD,
即BD=CE,
在△ABD与△FEC中,
 ,
,
∴△ABD≌△FEC(SAS),
∴∠ADB=∠FCE.
【点评】此题考查全等三角形的判定和性质,关键是根据等式的性质得出BD=CE,再利用全等三角形的判定和性质解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 ﹣
﹣
 =1.
=1.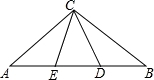
 )2•
)2• +
+ ÷
÷ .
.
