题目内容
周长相等的正三角形、正方形、正六边形、圆中，面积最大的是
- A.正三角形
- B.正方形
- C.正六边形
- D.圆
D
分析：要比较周长相等的正三角形、正方形、正六边形、圆中，面积最大的是什么图形，需分别计算出它们的面积；而正三角形、正方形、正六边形的面积都可以用其边长的代数式表示，圆的面积可以用半径的代数式表示，所以可设周长为L；用含L的代数式分别表示正三角形、正方形、正六边形的边长、圆的半径，从而可表示出正三角形、正方形、正六边形、圆的面积．
解答：设周长为L，根据题意得，正三角形、正方形、正六边形的边长分别为：
L，
L，
L，圆的半径为
L，
则正三角形、正方形、正六边形、圆的面积分别为：
×
L
L=
L2，
=
L2，
=
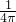L2，
=
L2．
所以，面积最大的是圆．
故选D．
点评：要熟练掌握正三角形、正方形、正六边形、圆的周长和面积公式．
分析：要比较周长相等的正三角形、正方形、正六边形、圆中，面积最大的是什么图形，需分别计算出它们的面积；而正三角形、正方形、正六边形的面积都可以用其边长的代数式表示，圆的面积可以用半径的代数式表示，所以可设周长为L；用含L的代数式分别表示正三角形、正方形、正六边形的边长、圆的半径，从而可表示出正三角形、正方形、正六边形、圆的面积．
解答：设周长为L，根据题意得，正三角形、正方形、正六边形的边长分别为：
L，L，L，圆的半径为L，则正三角形、正方形、正六边形、圆的面积分别为：
×LL=L2，=L2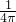，=L2，=L2．所以，面积最大的是圆．
故选D．
点评：要熟练掌握正三角形、正方形、正六边形、圆的周长和面积公式．
练习册系列答案
中考利剑中考试卷汇编系列答案
相关题目
周长相等的正三角形、正方形、正六边形、圆中，面积最大的是（ ）
| A、正三角形 | B、正方形 | C、正六边形 | D、圆 |