题目内容
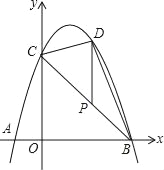
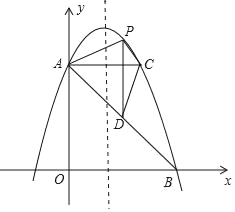
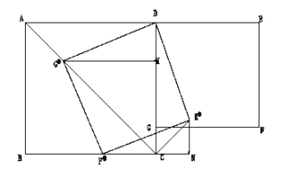
【题目】已知：矩形ABCD中，AB=4，BC=3，点M、N分别在边AB、CD上，直线MN交矩形对角线AC于点E，将△AME沿直线MN翻折，点A落在点P处，且点P在射线CB上
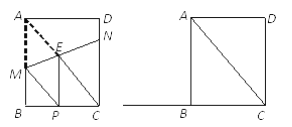
（I）如图①，当EP⊥BC时，①求证CE=CN；②求CN的长；
（II）请写出线段CP的长的取值范围，及当CP的长最大时MN的长。
【答案】（1）①见解析②
（2）O≤CP≤5，MN最大值为
【解析】
（1）先由折叠得出∠AEM=∠PEM，AE=PE，再判断出AB∥EP，进而判断出CN=CE,再利用锐角三角函数即可得出CN的长；（2）先确定出PC的最大值和最小值的位置，即可得出PC的范围，最后用折叠的性质与勾股定理即可得出结论.
（1）①∵△AME沿直线MN翻折，点A落在点P处，
∴△AME≌△PME，
∴∠AME=∠PEM，AE=PE，
∵四边形ABCD是矩形，
∴AB⊥BC，
∵EP⊥BC，
∴AB∥EP，
∴∠AME=∠PEM，
∴∠AEM=∠AME，
∴AM=AE,
∵四边形ABCD是矩形，
∴AB∥AE，
∴
∴CN=CE
②设CN=CE=x，
∵四边形ABCD是矩形，AB=4，BC=3，
∴AC=5，
∴PE=AE=5-x，
∵EP⊥BC，
∴
，
∴
∴x=
即CN=
（2）∵四边形ABCD是矩形，
∴∠ABC=90°，
在Rt△ABC中，AB=4，BC=3，根据勾股定理得AC=5，
由折叠可知AE=PE,
由三角形的三边关系得，PE+CE＞PC，
∴AC＞PC，
∴PC＜5，
∴点E是AC中点时，PC的最小为0，当点E和点C重合时，PC最大为AC=5，
∴O≤CP≤5，
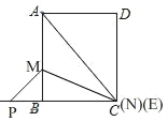
如图，当点C、N、E重合时，PC=BC+BP=5，
∴BP=2，
由折叠得PM=AM，
在Rt△PBM中，PM=4-BM，根据勾股定理得PM2-BM2=BP2，
∴(4-BM)2-BM2=42，
∴BM=
在Rt△BCM中，根据勾股定理得MN=
即当CP最大时，MN=.
