题目内容
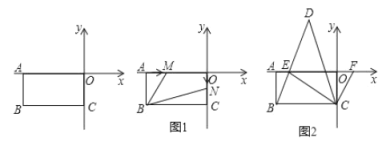
【题目】在平面直角坐标系中，A（a，0），C（0，c）且满足：
，长方形ABCO在坐标系中（如图）点O为坐标系的原点。
（1）求点B的坐标。
（2）如图1，若点M从点A出发，以2个单位/秒的速度向右运动（不超过点0），点N从原点O出发，以1个单位/秒的速度向下运动（不超过点C），设M、N两点同时出发，在它们运动的过程中，四边形MBNO的面积是否发生变化？若不变，求其值；若变化，求变化的范围。
（3）如图2，E为x轴负半轴上一点，且
，F是x轴正半轴上一动点，∠ECF的平分线CD交BE的延长线于点D，在点F运动的过程中，请探究∠CFE与∠D的数量关系并说明理由。
（注：三角形三个内角的和等于
）
【答案】（1）B（-6，-3）；（2）9；（3）
【解析】
（1）根据
可得
的值，由图可知点B的坐标；
（2）可设时间为t，用含t的式子表示出
，
，
，表示出四边形MBCN的面积求解即可；
（3）通过角之间的关系转化表示出
与
间的关系，可得结论.
解：（1）根据可得
，所以点B坐标为（-6，-3）；
（2）设时间为t，所以
，
，所以
，
四边形MBCN的面积
，与时间t无关，
所以四边形MBCN的面积不发生变化，其值为9.
（3）过点E作
交BC于点G，延长BC至H ，如图所示
由长方形ABCO可知
平分∠ECF
练习册系列答案
相关题目
