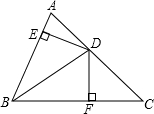
题目内容
如图,BE=CF,DE⊥AB的延长线于点E,DF⊥AC于点F,且DB=DC,
求证:AD是∠BAC的平分线.

【考点】角平分线的性质;垂线;直角三角形全等的判定;全等三角形的判定与性质.
【专题】探究型.
【分析】先根据全等三角形的判定定理得出Rt△BDE≌Rt△CDF,进而得出DE=DF,由角平分线的判定可知AD是∠BAC的平分线.
【解答】证明:∵DE⊥AB的延长线于点E,DF ⊥AC于点F,
⊥AC于点F,
∴∠BED=∠CFD,
∴△BDE与△CDF是直角三角形,
∵ ,
,
∴Rt△BDE≌Rt△CDF,
∴DE=DF,
∴AD是∠BAC的平分线.
【点评】本题考查的是角平分线的判定及全等三角形的判定与性质,熟知到角的两边的距离相等的点在角的平分线上是解答此题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 ( )
( )