Question

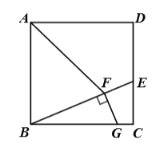
【题目】如图，已知Rt△ABC中，C=90°，O在AC上，以OC为半径作⊙O，切AB于D点，且BC=BD.

（1）求证：AB为⊙O的切线；

（2）若BC=6，sinA=，求⊙O的半径；

（3）在（2）的条件下，P点在⊙O上为一动点，求BP的最大值与最小值.

Answer 1

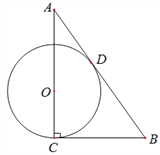
【答案】（1）连OD，证明略；（2）半径为3；（3）最大值3+3 ，3-3.

【解析】

（1）连接OD，OB，证明△ODB≌△OCB即可.

（2）由sinA=且BC=6可知，AB=10且cosA=，然后求出OD的长度即可.

（3）由三角形的三边关系，可知当连接OB交⊙O于点E、F，当点P分别于点E、F重合时，BP分别取最小值和最大值.

（1）如图：连接OD、OB.

在△ODB和△OCB中：

OD=OC,OB=OB,BC=BD;

∴△ODB≌△OCB（SSS）.

∴∠ODB=∠C=90°.

∴AB为⊙O的切线.

（2）如图：

∵sinA=，∴,

∵BC=6，∴AB=10,

∵BD=BC=6,

∴AD=AB-BD=4,

∵sinA=，∴cosA=，

∴OA=5，∴OD=3，

即⊙O的半径为：3.

（3）如图：连接OB，交⊙O为点E、F，

由三角形的三边关系可知：

当P点与E点重合时，PB取最小值.

由（2）可知：OD=3，DB=6,

∴OB=.

∴PB=OB-OE=.

当P点与F点重合时，PB去最大值，

PB=OP+OB=3+.