题目内容
在平行四边形 中,
中, 分别为边
分别为边 的中点,连接
的中点,连接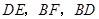 .
.
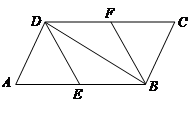
(1)求证: .(4分)
.(4分)
(2)若 ,则四边形
,则四边形 是什么特殊四边形?请证明你的结论.(5分)
是什么特殊四边形?请证明你的结论.(5分)
 中,
中, 分别为边
分别为边 的中点,连接
的中点,连接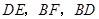 .
.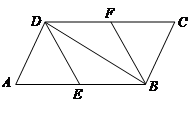
(1)求证:
 .(4分)
.(4分)(2)若
 ,则四边形
,则四边形 是什么特殊四边形?请证明你的结论.(5分)
是什么特殊四边形?请证明你的结论.(5分)证明见解析.
试题分析:(1)根据平行四边形的对边相等的性质可以得到AD=BC,AB=CD,又点E、F是AB、CD中点,所以AE=CF,然后利用边角边即可证明两三角形全等;
(2)先证明BE与DF平行且相等,然后根据一组对边平行且相等的四边形是平行四边形证明,连接EF,可以证明四边形AEFD是平行四边形,所以AD∥EF,又AD⊥BD,所以BD⊥EF,根据菱形的判定可以得到四边形是菱形.
试题解析:(1)在?ABCD中,AD=BC,AB=CD,∠A=∠C,
∵E、F分别为边AB、CD的中点,
∴AE=CF,
在△ADE和△CBF中,
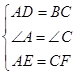 ,
,∴△ADE≌△CBF(SAS);
(2)是菱形.理由如下:
由(1)可得BE=DF,
又AB∥CD,
∴BE
 DF,
DF,∴四边形BEDF是平行四边形,
连接EF,在?ABCD中,E、F分别为边AB、CD的中点,

∴DF
 AE,
AE,∴四边形AEFD是平行四边形,
∴EF∥AD,
∵AD⊥BD,
∴EF⊥BD,
又∵四边形BFDE是平行四边形,
∴四边形BFDE是菱形.

练习册系列答案
相关题目

 ,延长BA至D,使
,延长BA至D,使 ,点E、F分别是边BC、AC的中点.
,点E、F分别是边BC、AC的中点.
 的边长1,面积为
的边长1,面积为 ,则
,则 的值为( )
的值为( )





 中,
中, 是
是 边上的中点.若
边上的中点.若 ,
, ,则平行四边形
,则平行四边形
