Question

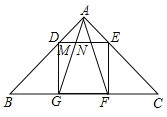
【题目】如图，在△ABC中，AB＝AC＝3，∠BAC＝90°，正方形DEFG的四个顶点在△ABC的边上，连接AG、AF分别交DE于点M和点N，则线段MN的长为_____．

Answer 1

【答案】．

【解析】

根据三角形的面积公式求出BC边上的高＝3，根据△ADE∽△ABC，求出正方形DEFG的边长为2，根据等于高之比即可求出MN．

解：作AQ⊥BC于点Q．

∵AB＝AC＝3，∠BAC＝90°，

∴BC＝AB＝6，

∵AQ⊥BC，

∴BQ＝QC，

∴BC边上的高AQ＝BC＝3，

∵DE＝DG＝GF＝EF＝BG＝CF，

∴DE：BC＝1：3

又∵DE∥BC，

∴AD：AB＝1：3，

∴AD＝，DE＝AD＝2，

∵△AMN∽△AGF，DE边上的高为1，

∴MN：GF＝1：3，

∴MN：2＝1：3，

∴MN＝．

故答案为.