题目内容
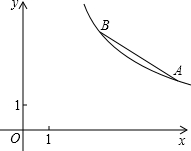 如图,反比例函数y=
如图,反比例函数y=| k |
| x |
| 10 |
(1)求A、B点的坐标及反比例函数解析式;
(2)如果M为x轴上一点,N为y轴上一点,以A、B、M、N为顶点的四边形是平行四边形,请直接写出符合条件的M、N点的坐标,并画出相应的平行四边形.
分析:(1)先由点A的坐标为(3m,m)及OA=2
,根据两点间距离公式列出关于m的方程,解方程求出m的值,再运用待定系数法得到k的值,然后将B点坐标代入,即可求出n的值;
(2)设M点坐标为(a,0),N点坐标为(0,b).分两种情况:①当M点和A点相邻时;②当M和B点相邻时.针对每一种情况,都可以根据平行四边形的对角线互相平分的性质及中点坐标公式求解.
| 10 |
(2)设M点坐标为(a,0),N点坐标为(0,b).分两种情况:①当M点和A点相邻时;②当M和B点相邻时.针对每一种情况,都可以根据平行四边形的对角线互相平分的性质及中点坐标公式求解.
解答:解:(1)∵A(3m,m),OA=2
,
∴(3m)2+m2=(2
)2,且m>0.
解得m=2.
∴A的坐标为(6,2).
又∵点A在y=
的图象上,
∴k=6×2=12.
∴反比例函数解析式为y=
.
∵点B(n,n+1)(其中n>0)在y=
的图象上,
∴n(n+1)=12.
解得n1=3,n2=-4(不合题意,舍去).
∴点的坐标为B(3,4);
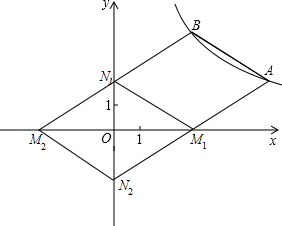 (2)设M点坐标为(a,0),N点坐标为(0,b),如图.
(2)设M点坐标为(a,0),N点坐标为(0,b),如图.
分两种情况:
①当M点和A点相邻时.
∵M1ABN1是平行四边形,
∴M1B与AN1互相平分,即M1B的中点与AN1的中点重合,
∴
=
,
=
,
∴a=3,b=2,
∴M1(3,0),N1(0,2);
②当M和B点相邻时.
∵N2ABM2是平行四边形,
∴M2A与BN2互相平分,即M2A的中点与BN2的中点重合,
∴
=
,
=
,
∴a=-3,b=-2,
∴M2(3,0),N2(0,-2).
综上可知,符合条件的M、N点的坐标分别为M1(3,0),N1(0,2)或M2(-3,0),N2(0,-2).
| 10 |
∴(3m)2+m2=(2
| 10 |
解得m=2.
∴A的坐标为(6,2).
又∵点A在y=
| k |
| x |
∴k=6×2=12.
∴反比例函数解析式为y=
| 12 |
| x |
∵点B(n,n+1)(其中n>0)在y=
| 12 |
| x |
∴n(n+1)=12.
解得n1=3,n2=-4(不合题意,舍去).
∴点的坐标为B(3,4);
 (2)设M点坐标为(a,0),N点坐标为(0,b),如图.
(2)设M点坐标为(a,0),N点坐标为(0,b),如图.分两种情况:
①当M点和A点相邻时.
∵M1ABN1是平行四边形,
∴M1B与AN1互相平分,即M1B的中点与AN1的中点重合,
∴
| a+3 |
| 2 |
| 0+6 |
| 2 |
| 0+4 |
| 2 |
| b+2 |
| 2 |
∴a=3,b=2,
∴M1(3,0),N1(0,2);
②当M和B点相邻时.
∵N2ABM2是平行四边形,
∴M2A与BN2互相平分,即M2A的中点与BN2的中点重合,
∴
| a+6 |
| 2 |
| 0+3 |
| 2 |
| b+4 |
| 2 |
| 0+2 |
| 2 |
∴a=-3,b=-2,
∴M2(3,0),N2(0,-2).
综上可知,符合条件的M、N点的坐标分别为M1(3,0),N1(0,2)或M2(-3,0),N2(0,-2).
点评:本题考查了运用待定系数法求反比例函数的解析式,反比例函数的性质及平行四边形的性质,两点间距离公式及中点坐标公式,综合性较强,有一定难度,注意分类讨论思想的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,反比例函数y=
如图,反比例函数y= 如图,反比例函数
如图,反比例函数 如图,反比例函数
如图,反比例函数 如图,反比例函数
如图,反比例函数 如图,反比例函数
如图,反比例函数