题目内容
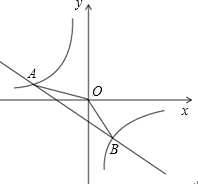 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y=| m | x |
(1)求反比例函数和一次函数的解析式;
(2)连接OA,OB求三角形OAB的面积.
分析:(1)因为反比例函数过A、B两点,所以可求其解析式和n的值,从而知B点坐标,进而求一次函数解析式;
(2)求出直线与一条坐标轴的交点坐标,将△OAB分割成两个三角形求面积.
(2)求出直线与一条坐标轴的交点坐标,将△OAB分割成两个三角形求面积.
解答:解:(1)x=-3,y=1代入y=
,
∴m=-3,
∴反比例函数的解析式为y=-
,
把x=2,y=n代入y=-
得n=-
.
把x=-3,y=1;x=2,y=-
分别代入
y=kx+b中:
得
,
解得
∴一次函数的解析式为y=-
x-
;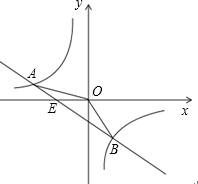
(2)设直线AB交x轴于点E,
∴E(-1,0)
则S△AOB=S△AEO+S△BOE=0.5+0.75=1.25.
| m |
| x |
∴m=-3,
∴反比例函数的解析式为y=-
| 3 |
| x |
把x=2,y=n代入y=-
| 3 |
| x |
| 3 |
| 2 |
把x=-3,y=1;x=2,y=-
| 3 |
| 2 |
y=kx+b中:
得
|
解得
|
∴一次函数的解析式为y=-
| 1 |
| 2 |
| 1 |
| 2 |

(2)设直线AB交x轴于点E,
∴E(-1,0)
则S△AOB=S△AEO+S△BOE=0.5+0.75=1.25.
点评:此题主要考查检查利用待定系数法确定函数关系式及图形的面积分割转化思想方法.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 已知,如图,一次函数y1=-x-1与反比例函数y2=-
已知,如图,一次函数y1=-x-1与反比例函数y2=-| 2 |
| x |
| A、x>1 |
| B、x<-2或0<x<1 |
| C、-2<x<1 |
| D、-2<x<0或x>1 |
 如图,一次函数y=kx+2的图象与反比例函数y=
如图,一次函数y=kx+2的图象与反比例函数y= 13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是
13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是 (2013•成都)如图,一次函数y1=x+1的图象与反比例函数
(2013•成都)如图,一次函数y1=x+1的图象与反比例函数 如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数
如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数