Question

【题目】如图，在△ABC中，AB=4，D是AB上的一点（不与点A、B重合），DE∥BC，交AC于点E，则 的最大值为 ．

Answer 1

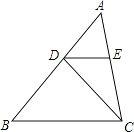
【答案】
【解析】解：设AD=x， =y， ∵AB=4，AD=x，
∴ =（ ）2=（ ）2 ，
∴ = x2①，
∵DE∥BC，
∴△ADE∽△ABC，
∴ = ，
∵AB=4，AD=x，
∴ = ，
∴ = ，
∵△ADE的边AE上的高和△CED的边CE上的高相等，
∴ = = ②，
①÷②得：
∴y= =﹣ x2+ x，
∵AB=4，
∴x的取值范围是0＜x＜4；
∴y= =﹣ （x﹣2）2+ ≤ ，
∴ 的最大值为 ．
所以答案是： ．
【考点精析】通过灵活运用二次函数的最值和相似三角形的判定与性质，掌握如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方即可以解答此题．