题目内容
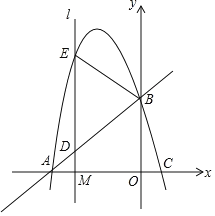
【题目】探测气球甲从海拔![]() 处出发,与此同时,探测气球乙从海拔
处出发,与此同时,探测气球乙从海拔![]() 处出发.图中的
处出发.图中的![]() 分别表示甲、乙两个气球所在位置的海拔
分别表示甲、乙两个气球所在位置的海拔![]() (单位:
(单位:![]() )与上升时间
)与上升时间![]() (单位:
(单位:![]() )之间的关系.
)之间的关系.
(1)求![]() 的函数解析式;
的函数解析式;
(2)探测气球甲从出发点上升到海拔![]() 处的过程中,是否存在某一时刻使得探测气球甲、乙位于同一高度?请说明理由.
处的过程中,是否存在某一时刻使得探测气球甲、乙位于同一高度?请说明理由.
【答案】(1)s=![]() t+6(t≥0);(2)探测气球甲从出发点上升到海拔16m处的过程中,当上升15min时探测气球甲、乙位于同一高度,见解析
t+6(t≥0);(2)探测气球甲从出发点上升到海拔16m处的过程中,当上升15min时探测气球甲、乙位于同一高度,见解析
【解析】
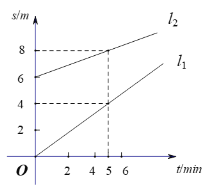
(1)设l2的解析式为s=k2t+b(k2≠0),根据t=0时,s=6、当t=5时,s=8直接列方程组,求解即可;
(2)先根据题意求出![]() 的解析式,联立l1和l2,求出此时的t值,经验证满足题意,即可求解本题.
的解析式,联立l1和l2,求出此时的t值,经验证满足题意,即可求解本题.
(1)解:由题可设l2的解析式为s=k2t+b(k2≠0)
因为当t=0时,s=6、当t=5时,s=8,
代入得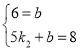 ,
,
解得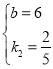 ,
,
所以l2:s=![]() t+6(t≥0);
t+6(t≥0);
(2)解:由题可设l1:s=k1t(k1≠0),
因为当t=5时,s=4,
代入可得l1:s=![]() t(t≥0)
t(t≥0)
当二者处于同一高度时,
![]() t+6=
t+6=![]() t,
t,
解得t=15,
此时s=12,
即在15min时,二者处于同一高度12m;
因为12m<16m,
所以探测气球甲从出发点上升到海拔16m处的过程中,当上升15min时,探测气球甲、乙位于同一高度;
答:探测气球甲从出发点上升到海拔16m处的过程中,当上升15min时探测气球甲甲、乙位于同一高度.

练习册系列答案
相关题目