题目内容
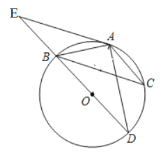
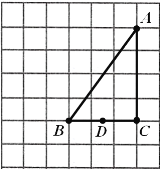
【题目】如图，在由边长都为1的小正方形组成的网格中，点
，
，
均为格点，
，
，
，
为
中点，
为
上的一个动点．
（1）当点为线段中点时，
的长度等于__________；
（2）将点绕点逆时针旋转90°得到点
，连
，当线段
取得最小值时，请借助无刻度直尺在给定的网格中画出点，点，并简要说明你是怎么画出点，点的：____________________．
【答案】（1）
；（2）图见解析；取格点
，
，
，
，连接
，
，它们分别与网格线相交于点
，
，取格点
，连接
，
，它们相交于点
，则点即为所求；取格点
，
，连接
，与网格线相交于点
，连接
，与网格线相交于点
，则点即为所求．
【解析】
（1）根据勾股定理先求出AB的长，再利用中位线定理可得出DP的长；
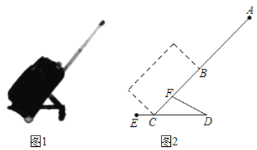
（2）如图1，设P为AC上任意一点，过点P′作P′C′⊥CB交其延长线与点C′，易得△CDP≌△C′P′D，得出P′C′=CD=
，从而可得出点P′一定在直线l上，再找出点B关于直线l的对称点K，连接DK与l的交点即可点P′，此时
的值最小，因此根据平行四边形的判定与性质以及全等三角形的判定与性质先作出直线l（或在直线l上的线段），利用轴对称的性质可得出点K，进而可得出点；利用旋转的性质以及全等三角形的判定与性质在AC上找一点P，使△CDP≌△QKP′，则有DP=KP′=DP′，即可得出点P．
解：（1）根据勾股定理得，AB=
，
又点D为BC的中点，点P为AC的中点，
∴DP为△ABC的中位线，
∴DP=
AB=．
故答案为：；
（2）如图1，设P为AC上任意一点，过点P′作P′C′⊥CB交其延长线与点C′，
根据题意可得，DP=DP′，∠PDP′=90°，
∴易得△CDP≌△C′P′D，∴P′C′=CD=，
∴点P′一定在直线l上，
∴再找出点B关于直线l的对称点K，连接DK与l的交点即可点P′，此时的值最小．
如图2，取格点，，，，连接，，它们分别与网格线相交于点，，取格点，连接，，它们相交于点，则点即为所求；
取格点，，连接，与网格线相交于点，连接，与网格线相交于点，则点即为所求．
故答案为：取格点，，，，连接，，它们分别与网格线相交于点，，取格点，连接，，它们相交于点，则点即为所求；取格点，，连接，与网格线相交于点，连接，与网格线相交于点，则点即为所求．
