题目内容
点（-4，y1），（-2，y2），（1，y3）都在反比例函数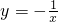
的图象上，则y1、y2、y3的大小关系为________（用“＜”号连接）．
y3＜y1＜y2
分析：由反比例函数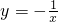的解析式可知函数的图象在二、四象限，由三点的横坐标可知（-4，y1），（-2，y2）在第二象限，（1，y3）在第四象限，根据反比例函数的增减性及各象限内点的坐标特点即可解答．
解答：∵反比例函数y=-
中k=-1＜0，∴此函数的图象在二、四象限，
∵-4＜0，-2＜0，1＞0，
∴（-4，y1），（-2，y2）在第二象限，（1，y3）在第四象限，
∴y1＞0，y2＞0，y3＜0，
∵-4＜-2，
∴y2＞y1＞0，
∴y3＜y1＜y2．
点评：此题比较简单，解答此题的关键是熟知反比例函数的性质及平面直角坐标系中各象限内点的坐标特点，属较简单题目．
分析：由反比例函数
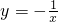的解析式可知函数的图象在二、四象限，由三点的横坐标可知（-4，y1），（-2，y2）在第二象限，（1，y3）在第四象限，根据反比例函数的增减性及各象限内点的坐标特点即可解答．解答：∵反比例函数y=-
中k=-1＜0，∴此函数的图象在二、四象限，∵-4＜0，-2＜0，1＞0，
∴（-4，y1），（-2，y2）在第二象限，（1，y3）在第四象限，
∴y1＞0，y2＞0，y3＜0，
∵-4＜-2，
∴y2＞y1＞0，
∴y3＜y1＜y2．
点评：此题比较简单，解答此题的关键是熟知反比例函数的性质及平面直角坐标系中各象限内点的坐标特点，属较简单题目．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
若点（-2，y1）（-1，y2）、（1，y3）都在反比例函数y=-
的图象上，则有（ ）
| 1 |
| x |
| A、y1＞y2＞y3 |
| B、y2＞y1＞y3 |
| C、y3＞y1＞y2 |
| D、yl＞y3＞y2 |