题目内容
【题目】甲、乙两车分别从
、
两地同时出发，甲车匀速前往地，到达地立即以另一速度按原路匀速返回到地；乙车匀速前往地，设甲、乙两车距离地的距离为
. 甲车行驶的时间为
，
与
之间的函数图象如图所示.
（1）甲车从地前往地的速度为_______
.
（2）求甲车返回时与之间的函数关系式，并写出自变量的取值范围.
（3）当甲、乙两车相距
时，直接写出甲车行驶的时间.
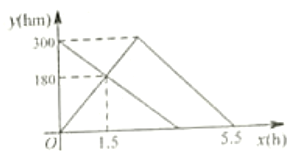
【答案】（1）120；（2）
，自变量
取值范围为：
；（3）
小时（或
），
小时（或
），
小时．
【解析】
（1）甲车从
地前往
地的速度为 120 
．
（2）法一：
设
， 把
，
代入
，
解得
自变量的取值范围为：．
法二：
设
，
把代入，
解得
∴
自变量取值范围为：．
（3）小时（或），小时（或），小时．
【题目】某商场的运动服装专柜，对
两种品牌的远动服分两次采购试销后，效益可观，计划继续采购进行销售．已知这两种服装过去两次的进货情况如下表．
第一次 | 第二次 | |
| 20 | 30 |
| 30 | 40 |
累计采购款/元 | 10200 | 14400 |
（1）问两种品牌运动服的进货单价各是多少元？
（2）由于
品牌运动服的销量明显好于
品牌，商家决定采购品牌的件数比品牌件数的
倍多5件，在采购总价不超过21300元的情况下，最多能购进多少件品牌运动服？
【题目】温州某企业安排65名工人生产甲、乙两种产品，每人每天生产2件甲或1件乙，甲产品每件可获利15元．根据市场需求和生产经验，乙产品每天产量不少于5件，当每天生产5件时，每件可获利120元，每增加1件，当天平均每件获利减少2元．设每天安排x人生产乙产品．
（1）根据信息填表
产品种类 | 每天工人数（人） | 每天产量（件） | 每件产品可获利润（元） |
甲 | 15 | ||
乙 |
|
|
（2）若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元，求每件乙产品可获得的利润．
（3）该企业在不增加工人的情况下，增加生产丙产品，要求每天甲、丙两种产品的产量相等．已知每人每天可生产1件丙（每人每天只能生产一件产品），丙产品每件可获利30元，求每天生产三种产品可获得的总利润W（元）的最大值及相应的x值．
